题目内容
某地绿化治理沙漠需要大量用水,第1年的用水量约为100(百吨),第2年的用水量约为120(百吨).该地政府综合各种因素预测:①每年的用水量会逐年增加;②每年的用水量都不能达到130(百吨).某校数学兴趣小组想找一个函数y=f(x)来拟合该项目第x(x≥1)年与当年的用水量y(单位:百吨)之间的关系,则函数y=f(x)必须符合预测①:f(x)在[1,+∞)上单调递增;预测②:f(x)<130对x∈[1,+∞)恒成立.
(1)若f(x)=
+n,试确定m,n的值,并考察该函数是否符合上述两点预测;
(2)若f(x)=a•bx+c(b>0,b≠1),欲使得该函数符合上述两点预测,试确定b的取值范围.
(1)若f(x)=
| m |
| x |
(2)若f(x)=a•bx+c(b>0,b≠1),欲使得该函数符合上述两点预测,试确定b的取值范围.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)根据题意可知,点(1,100)和(2,120)均在函数f(x)上,代入即可求得m,n的值,确定函数f(x)=-
+140,根据反比例函数的性质,即可确定f(x)的单调性,和f(x)的取值范围,对应预测①②,即可判断出答案;
(2)根据题意可知,点(1,100)和(2,120)均在函数f(x)上,代入即可求得a与b的关系,c与b的关系,将a和c都用b来表示,得到f(x)的解析式,要满足预测①,则f′(x)>0,确定出两种情况,对两种情况分别研究预测②的恒成立问题,即可求得实数b的取值范围.
| 40 |
| x |
(2)根据题意可知,点(1,100)和(2,120)均在函数f(x)上,代入即可求得a与b的关系,c与b的关系,将a和c都用b来表示,得到f(x)的解析式,要满足预测①,则f′(x)>0,确定出两种情况,对两种情况分别研究预测②的恒成立问题,即可求得实数b的取值范围.
解答:
解:(1)将(1,100)、(2、120)代入到f(x)=
+n中,得
,
解得m=-40,n=140,
∵f(x)=-
+140,
∴f′(x)=
>0,
故f(x)在[1,+∞) 上单调递增,符合预测①;
又当x≥4 时,f(x)=-
+140≥130,
∴此时f(x)不符合预测②;
(2)∵f(x)=a•bx+c(b>0,b≠1),
将(1,100)、(2、120)代入到f(x)=a•bx+c,
∴
,解得a=
,c=100-
,
∴f′(x)=abxlnb,要想符合预测①,则f′(x)>0,
∴alnb>0,
∴
或
,
①当b>1时,a=
>0,此时符合预测①,
但由f(x)≥130,解得x≥logb(
b2-
),
即当x≥logb(
b2-
)时,f(x)≥130,
∴此时f(x)不符合预测②;
②当0<b<1,a=
<0,此时符合预测①,
又由x≥1,知bx∈(0,b],
∴abx∈[ab,0),
∴f(x)∈[ab+c,c),
要使得f(x)也符合预测②,则c≤130,
∴100-
≤130,
又0<b<1,解得0<b≤
.
综上所述,b的取值范围是(0,
].
| m |
| x |
|
解得m=-40,n=140,
∵f(x)=-
| 40 |
| x |
∴f′(x)=
| 40 |
| x2 |
故f(x)在[1,+∞) 上单调递增,符合预测①;
又当x≥4 时,f(x)=-
| 40 |
| x |
∴此时f(x)不符合预测②;
(2)∵f(x)=a•bx+c(b>0,b≠1),
将(1,100)、(2、120)代入到f(x)=a•bx+c,
∴
|
| 20 |
| b(b-1) |
| 2 |
| b-1 |
∴f′(x)=abxlnb,要想符合预测①,则f′(x)>0,
∴alnb>0,
∴
|
|
①当b>1时,a=
| 20 |
| b(b-1) |
但由f(x)≥130,解得x≥logb(
| 3 |
| 2 |
| b |
| 2 |
即当x≥logb(
| 3 |
| 2 |
| b |
| 2 |
∴此时f(x)不符合预测②;
②当0<b<1,a=
| 20 |
| b(b-1) |
又由x≥1,知bx∈(0,b],
∴abx∈[ab,0),
∴f(x)∈[ab+c,c),
要使得f(x)也符合预测②,则c≤130,
∴100-
| 20 |
| b-1 |
又0<b<1,解得0<b≤
| 1 |
| 3 |
综上所述,b的取值范围是(0,
| 1 |
| 3 |
点评:本题主要考查函数模型的选择与应用.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.本题考查了运用函数、导数的知识解决实际问题的能力.对于函数的恒成立问题,一般选用参变量分离法、最值法、数形结合法进行求解.属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若用m,n表示两条不同的直线,用α表示一个平面,则下列命题正确的是( )
| A、若m∥n,n?α,则m∥α |
| B、若m∥α,n?α,则m∥n |
| C、若m⊥n,n?α,则m⊥α |
| D、若m⊥α,n?α,则m⊥n |
若对任意一点O和不共线的三点A、B、C有
=x
+y
+z
,则x+y+z=1是四点P、A、B、C共面的( )
| OP |
| OA |
| OB |
| OC |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如图,正四面体ABCD的棱长为2,点E,F分别为棱BC,AD的中点,则
•
的值为( )
| EF |
| BA |

| A、4 | B、-4 | C、-2 | D、2 |
若f(x)是定义在R上的增函数,则对任意x、y∈R,“f(x)+f(y)<f(-x)+f(-y)”是“x+y<0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
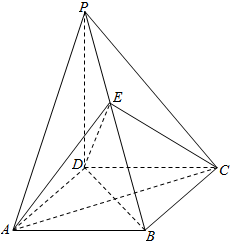 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=