题目内容
15.若θ∈(0,π),且sinθ+cosθ=0.2,则曲线x2sinθ+y2cosθ=1是( )| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
分析 把sinθ+cosθ=0.2两边平方可得,sinθ•cosθ=-0.48<0,可判断θ为钝角,cosθ<0,从而判断方程所表示的曲线.
解答 解:因为θ∈(0,π),且sinθ+cosθ=0.2,
所以,两边平方可得,sinθ•cosθ=-0.48<0
所以θ∈($\frac{π}{2}$,π),且|sinθ|>|cosθ|,
所以sinθ>0,cosθ<0,
从而x2sinθ+y2cosθ=1表示焦点在x轴上的双曲线.
故选:C.
点评 本题考查双曲线的标准方程形式,由三角函数式判断角的取值范围.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
3.已知$\frac{1+2i}{a+bi}$=1-i(i为虚数单位,a,b∈R),则|a+bi|=( )
| A. | $\frac{1}{2}+\frac{3}{2}i$ | B. | 1 | C. | 2 | D. | $\frac{{\sqrt{10}}}{2}$ |
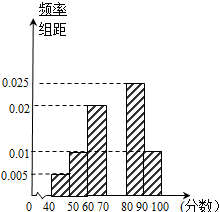 某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.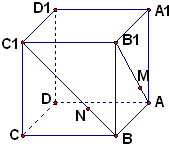 在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论:
在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论: