题目内容
16.记max{x,y}=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若f(x),g(x)均是定义在实数集R上的函数,定义函数h(x)=max{f(x),g(x)},则下列命题正确的是( )| A. | 若f(x),g(x)都是单调函数,则h(x)也是单调函数 | |
| B. | 若f(x),g(x)都是奇函数,则h(x)也是奇函数 | |
| C. | 若f(x),g(x)都是偶函数,则h(x)也是偶函数 | |
| D. | 若f(x)是奇函数,g(x)是偶函数,则h(x)既不是奇函数,也不是偶函数 |
分析 根据题意,通过举例说明选项中的命题是否成立即可.
解答 解:对于A,如f(x)=x,g(x)=-2x都是R上的单调函数,
而h(x)=$\left\{\begin{array}{l}{x,x≥0}\\{-2x,x<0}\end{array}\right.$不是定义域R上的单调函数,命题A错误;
对于B,如f(x)=x,g(x)=-2x都是R上的奇函数,
而h(x)=$\left\{\begin{array}{l}{x,x≥0}\\{-2x,x<0}\end{array}\right.$不是定义域R上的奇函数,命题B错误;
对于C,当f(x)、g(x)都是定义域R上的偶函数时,
h(x)=man{f(x),g(x)}也是定义域R上的偶函数,命题C正确;
对于D,如f(x)=sinx是定义域R上的奇函数,g(x)=x2+2是定义域R上的偶函数,
而h(x)=g(x)=x2+2是定义域R上的偶函数,命题D错误.
故选:C.
点评 本题考查了新定义的函数的性质与应用问题,主要根据定义判定函数的单调性与奇偶性的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知函数f(x=$\left\{\begin{array}{l}{f(x+2),x<2}\\{(\frac{1}{3})^{x},x≥2}\end{array}\right.$,f(-1+log35)的值为( )
| A. | $\frac{1}{15}$ | B. | $\frac{5}{3}$ | C. | 15 | D. | $\frac{2}{3}$ |
4.若命题P:所有的对数函数都是单调函数,则¬P为( )
| A. | 所有对数函数都不是单调函数 | B. | 所有的单调函数都不是对数函数 | ||
| C. | 存在一个对数函数不是单调函数 | D. | 存在一个单调函数都不是对数函数 |
8.据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3000人进行调查,就“是否取消英语听力”的问题进行了问卷调查统计,结果如表:
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.06.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.
| 态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 500人 | x人 | z人 |
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.
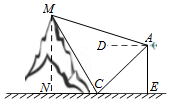 如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m.
如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m.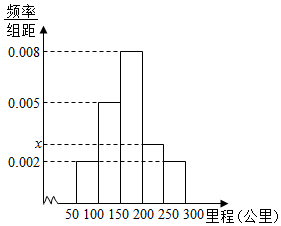 2015年1月1日新《环境保护法》实施后,2015年3月18日,交通运输部发布《关于加快推进新能源汽车在交通运输行业推广应用的实施意见》,意见指出,至2020年,新能源汽车在交通运输行业的应用初具规模,在城市公交、出租汽车和城市物流配送等领域的总量达到30万辆;新能源汽车配套服务设施基本完备,新能源汽车运营效率和安全水平明显提升.随着新能源汽车的迅速发展,关于新能源汽车是纯电动汽车的续航里程(单次充电后能行驶的最大里程)一直是消费者最为关注的话题.
2015年1月1日新《环境保护法》实施后,2015年3月18日,交通运输部发布《关于加快推进新能源汽车在交通运输行业推广应用的实施意见》,意见指出,至2020年,新能源汽车在交通运输行业的应用初具规模,在城市公交、出租汽车和城市物流配送等领域的总量达到30万辆;新能源汽车配套服务设施基本完备,新能源汽车运营效率和安全水平明显提升.随着新能源汽车的迅速发展,关于新能源汽车是纯电动汽车的续航里程(单次充电后能行驶的最大里程)一直是消费者最为关注的话题.