题目内容
8.据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3000人进行调查,就“是否取消英语听力”的问题进行了问卷调查统计,结果如表:| 态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 500人 | x人 | z人 |
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.
分析 (Ⅰ)先由抽到持“应该保留”态度的人的概率为0.06,由已知条件求出x,再求出持“无所谓”态度的人数,由此利用抽样比能求出应在“无所谓”态度抽取的人数.
(Ⅱ)先根据分层抽样,求出在校学生和社会人士的人数,再计算出这6人中任意选取2人的情况总数,及满足恰好有1个人为在校学生的情况数,代入古典概率概率计算公式,可得答案.
解答 解:(Ⅰ)∵抽到持“应该保留”态度的人的概率为0.06,
∴$\frac{120+x}{3000}$=0.06,解得x=60.
∴持“无所谓”态度的人数共有3000-2100-500-120-60=220.
∴应在“无所谓”态度抽取220×$\frac{300}{3000}$=22人.
(Ⅱ)由(Ⅰ)知持“应该保留”态度的一共有180人,
∴在所抽取的6人中,在校学生为$\frac{120}{180}$×6=4人,分别记为1,2,3,4,社会人士为$\frac{60}{180}$×6=2人,记为a,b,
则这6人中任意选取2人,共有15种不同情况,分别为:
(1,2),(1,3),(1,4),(1,a),(1,b),
(2,3),(2,4),(2,a),(2,b),(3,4),
(3,a),(3,b),(4,a),(4,b),(a,b),
这2人中恰好有1个人为在校学生:
(1,a),(1,b),(2,a),(2,b),(3,a),
(3,b),(4,a),(4,b),共8种.
故这2人中恰好有1个人为在校学生的概率为P=$\frac{8}{15}$
点评 本题主要考查古典概型及其概率计算公式的应用,列举法,是解决古典概型问题的一种重要的解题方法.还考查了分层抽样的定义和方法,属于基础题

练习册系列答案
相关题目
19.已知复数$z=\frac{1-i}{1+i}$,则z2016=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
16.记max{x,y}=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若f(x),g(x)均是定义在实数集R上的函数,定义函数h(x)=max{f(x),g(x)},则下列命题正确的是( )
| A. | 若f(x),g(x)都是单调函数,则h(x)也是单调函数 | |
| B. | 若f(x),g(x)都是奇函数,则h(x)也是奇函数 | |
| C. | 若f(x),g(x)都是偶函数,则h(x)也是偶函数 | |
| D. | 若f(x)是奇函数,g(x)是偶函数,则h(x)既不是奇函数,也不是偶函数 |
20.盒中共有6件除了颜色外完全相同的产品,其中有1件红色,2件白色和3件黑色,从中任取两件,则两件颜色不相同的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{7}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{11}{15}$ |
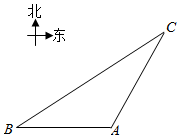 如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;
如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;