题目内容
已知命题p：方程2x2+ax-a2=0在[-1，1]上有解；命题q：只有一个实数x0满足不等式x02+2ax+2a≤0，若命题“p∨q”是假命题，求a的取值范围．
考点：复合命题的真假
专题：推理和证明
分析：首先求出命题p与q的等价命题，再根据命题“p∨q”是假命题求解即可．
解答：
解：由2x2+ax-a2=0，得（2x-a）（x+a）=0，∴x=
或x=-a，
∴当命题p为真命题时，|
|≤1或|-a|≤1，∴|a|≤2．即p?-2≤a≤2
又“只有一个实数x0满足不等式x
+2ax0+2a≤0”，
即抛物线y=x2+2ax+2a与x轴只有一个交点，
∴△=4a2-8a=0，∴a=0或a=2．
即q?a=0或a=2．
∴命题“p∨q”为真命题时，|a|≤2．
∵命题“p∨q”为假命题，∴a＞2或a＜-2．
即a的取值范围为（-∞，-2）∪（2，+∞）．
| a |
| 2 |
∴当命题p为真命题时，|
| a |
| 2 |
又“只有一个实数x0满足不等式x
2 0 |
即抛物线y=x2+2ax+2a与x轴只有一个交点，
∴△=4a2-8a=0，∴a=0或a=2．
即q?a=0或a=2．
∴命题“p∨q”为真命题时，|a|≤2．
∵命题“p∨q”为假命题，∴a＞2或a＜-2．
即a的取值范围为（-∞，-2）∪（2，+∞）．
点评：本题借助命题考查才一元二次方程的区间根问题，属于基础题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
已知向量
=（2k-3，-6），
=（2，1）且
∥
则实数k=（ ）
| a |
| c |
| a |
| c |
A、-
| ||
B、
| ||
| C、15 |
把十进制数15化为二进制数为（ ）
| A、1 011（2） |
| B、1 001（2） |
| C、1 111（2） |
| D、1 101（2） |
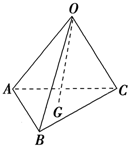如图，在三棱锥O-ABC中，G是△ABC的重心，若| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| OG |
A、
| ||||||
B、
| ||||||
| C、a+b+c | ||||||
| D、3a+3b+3c |