题目内容
3.已知集合A={x|(x-2)(x+6)<0},B={x|y=$\sqrt{1-x}$},则A∩B=( )| A. | (-6,1) | B. | (-6,1] | C. | (1,2) | D. | [1,2) |
分析 先分别求出集合A和B,由此利用交集定义能出A∩B.
解答 解:∵集合A={x|(x-2)(x+6)<0}={x|-6<x<2},
B={x|y=$\sqrt{1-x}$}={x|x≤1},
∴A∩B={x|-6<x≤1}=(-6,1].
故选:B.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
相关题目
14.函数f(x)=$\frac{1}{4}$sinxcosx是( )
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
8.把复数z的共轭复数记作$\overline{z}$,若(1+i)z=1-i,i为虚数单位,则$\overline{z}$=( )
| A. | i | B. | -i | C. | 1-i | D. | 1+i |
12.已知实数x、y满足$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,则z=x-y的取值范围是( )
| A. | [0,3] | B. | [-$\frac{17}{5}$,3] | C. | [-$\frac{17}{5}$,1] | D. | [-$\frac{17}{5}$,0] |
13.某城市理论预测2020年到2024年人口总数与年份的关系如下表所示
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(Ⅱ)据此估计2025年该城市人口总数.
参考数值:0×5+1×7+2×8+3×11+4×19=132,02+12+22+32+42=30,
参考公式:用最小二乘法求线性回归方程系数公式 $\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
| 年份202x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数 y(十万) | 5 | 7 | 8 | 11 | 19 |
(Ⅱ)据此估计2025年该城市人口总数.
参考数值:0×5+1×7+2×8+3×11+4×19=132,02+12+22+32+42=30,
参考公式:用最小二乘法求线性回归方程系数公式 $\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
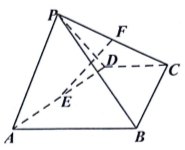 如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.
如图,在四棱锥P-ABCD中,△PAD为正三角形,四边形ABCD为直角梯形,CD∥AB,BC⊥AB,平面PAD⊥平面ABCD,点E、F分别为AD、CP的中点,AD=AB=2CD=2.