题目内容
5.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左右焦点分别为F1,F2,直线l经过点F1及虚轴的一个端点,且点F2到直线l的距离等于实半轴的长,则双曲线的离心率为( )| A. | $\frac{{1+\sqrt{5}}}{2}$ | B. | $\frac{{3+\sqrt{5}}}{4}$ | C. | $\sqrt{\frac{{1+\sqrt{5}}}{2}}$ | D. | $\frac{{\sqrt{3+\sqrt{5}}}}{2}$ |
分析 利用点F2到直线l的距离等于实半轴的长,可得$\frac{|2bc|}{\sqrt{{b}^{2}+{c}^{2}}}$=a,得出a与c之间的等量关系,进而求出离心率.
解答 解:由题意,直线l的方程为y=$\frac{b}{c}$x+b,即bx-cy+bc=0,
∵点F2到直线l的距离等于实半轴的长,
∴$\frac{|2bc|}{\sqrt{{b}^{2}+{c}^{2}}}$=a,
∴4(c2-a2)c2=a2(2c2-a2),
∴4e4-6e2+1=0,
∵e>1,∴e=$\frac{\sqrt{3+\sqrt{5}}}{2}$,
故选D.
点评 本题考查双曲线的方程与性质,考查点到直线距离公式的运用,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
16.已知集合A={1,2,3},B={x|x2-x-6=0},则A∩B=( )
| A. | {1} | B. | {2} | C. | {3} | D. | {2,3} |
13.已知-1,a1,a2,-9成等差数列,-9,b1,b2,b3,-1成等比数列,则b2(a2-a1)的值为( )
| A. | 8 | B. | -8 | C. | ±8 | D. | $±\frac{9}{8}$ |
17.已知圆C:(x-1)2+(y-2)2=2与y轴在第二象限所围区域的面积为S,直线y=3x+b分圆C的内部为两部分,其中一部分的面积也为S,则b=( )
| A. | -1±$\sqrt{10}$ | B. | 1$±\sqrt{10}$ | C. | -1-$\sqrt{10}$ | D. | 1-$\sqrt{10}$ |
15.已知点A是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a,b>0)右支上一点,F是右焦点,若△AOF(O是坐标原点)是等边三角形,则该双曲线离心率e为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
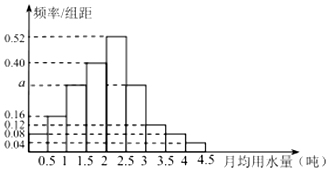 我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超过x的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超过x的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.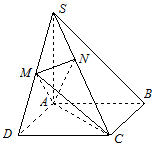 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N. 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.