题目内容
2.《九章算术》是我国古代数学名著,也是古代东方数学的代表作.书中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其意思为:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”现若向此三角形内投豆子,则落在其内切圆内的概率是( )| A. | $\frac{3π}{10}$ | B. | $\frac{π}{20}$ | C. | $\frac{3π}{20}$ | D. | $\frac{π}{10}$ |
分析 利用直角三角形三边与内切圆半径的关系求出半径,然后分别求出三角形和内切圆的面积,根据几何概型的概率公式即可求出所求.
解答 解:由题意,直角三角形,斜边长为17,由等面积,可得内切圆半径r=$\frac{8×15}{8+15+17}$=3,
∴向此三角形内投豆子,则落在其内切圆内的概率是$\frac{π•{3}^{2}}{\frac{1}{2}×8×15}$=$\frac{3π}{20}$,
故选C.
点评 本题考查直角三角形内切圆的有关知识,以及几何概型的概率公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.抛物线x2=4y上一点A的纵坐标为4,则点A与抛物线焦点的距离为( )
| A. | 5 | B. | 4 | C. | $\sqrt{15}$ | D. | $\sqrt{10}$ |
13.已知-1,a1,a2,-9成等差数列,-9,b1,b2,b3,-1成等比数列,则b2(a2-a1)的值为( )
| A. | 8 | B. | -8 | C. | ±8 | D. | $±\frac{9}{8}$ |
17.已知圆C:(x-1)2+(y-2)2=2与y轴在第二象限所围区域的面积为S,直线y=3x+b分圆C的内部为两部分,其中一部分的面积也为S,则b=( )
| A. | -1±$\sqrt{10}$ | B. | 1$±\sqrt{10}$ | C. | -1-$\sqrt{10}$ | D. | 1-$\sqrt{10}$ |
7.为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
( I)求a,b的值及随机抽取一考生恰为优秀生的概率;
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.05 |
| [60,70) | a | 0.20 |
| [70,80) | 35 | b |
| [80,90) | 25 | 0.25 |
| [90,100) | 15 | 0.15 |
| 合计 | 100 | 1.00 |
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
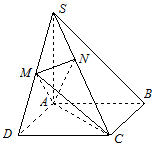 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N. 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.