题目内容
在直角坐标系中,曲线C的参数方程为
(φ为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点P(
,
),直线l的极坐标方程为ρ=
.
(1)判断点P与直线l的位置关系,说明理由;
(2)设直线l与曲线C的两个交点为A、B,求|PA|•|PB|的值.
|
| 3 |
| π |
| 2 |
| ||
2cos(θ-
|
(1)判断点P与直线l的位置关系,说明理由;
(2)设直线l与曲线C的两个交点为A、B,求|PA|•|PB|的值.
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)把直线直线l的极坐标方程化为直角坐标方程,再根据点P的直角坐标满足直线的方程,可得点P(0,
)在直线l上.
(2)把直线l的参数方程代入曲线C的直角坐标方程,可得 t2+2t-8=0,则由韦达定理可得 t1•t2=-8,从而求得|PA|•|PB|=|t1•t2|的值.
| 3 |
(2)把直线l的参数方程代入曲线C的直角坐标方程,可得 t2+2t-8=0,则由韦达定理可得 t1•t2=-8,从而求得|PA|•|PB|=|t1•t2|的值.
解答:
解:(1)直线直线l的极坐标方程为ρ=
即
ρcosθ+ρsinθ=
,
故直线l的直角坐标方程为
x+y=
,再根据点P的直角坐标为(0,
),满足直线的方程,
故点P(0,
)在直线l上.
(2)直线l的参数方程为
(t为参数),曲线C的直角坐标方程为
+
=1,
将直线l的参数方程代入曲线C的直角坐标方程,可得 t2+2t-8=0,
设两根为t1、t2,则由韦达定理可得 t1•t2=-8,∴|PA|•|PB|=|t1•t2|=8.
| ||
2cos(θ-
|
| 3 |
| 3 |
故直线l的直角坐标方程为
| 3 |
| 3 |
| 3 |
故点P(0,
| 3 |
(2)直线l的参数方程为
|
| x2 |
| 5 |
| y2 |
| 15 |
将直线l的参数方程代入曲线C的直角坐标方程,可得 t2+2t-8=0,
设两根为t1、t2,则由韦达定理可得 t1•t2=-8,∴|PA|•|PB|=|t1•t2|=8.
点评:本题主要考查把极坐标方程、参数方程化为直角坐标方程的方法,参数的几何意义,韦达定理的应用,属于基础题.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
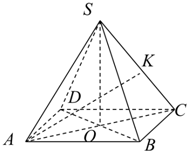 如图,四棱锥S-ABCD的高为2,底面ABCD是边长为
如图,四棱锥S-ABCD的高为2,底面ABCD是边长为