题目内容
已知函数f(x)=sin2x+2
cos2x-2a(x∈[0,
])有唯一的一个零点,则实数a的取值范围是 .
| 3 |
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:利用三角恒等变换可得f(x)=2sin(2x+
)-2a,由f(x)=0可得2sin(2x+
)=2a-
,x∈[0,
]⇒
≤2x+
≤
,利用正弦函数的图象与性质即可求得-
≤2sin(2x+
)≤2,进一步即可求得实数a的取值范围.
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| 3 |
| π |
| 3 |
解答:
解:由f(x)=sin2x+2
cos2x-2a=sin2x+
cos2x+
-2a=0,得2sin(2x+
)=2a-
,
∵x∈[0,
],
∴
≤2x+
≤
,
∴-
≤2sin(2x+
)≤2.
依题意知,
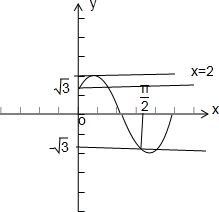
-
≤2a-
<
,或2a-
=2,
解得:0≤a<
或a=
,
∴实数a的取值范围是{a|0≤a<
或
},
故答案为:{a|0≤a<
或
}.
| 3 |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
∵x∈[0,
| π |
| 2 |
∴
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴-
| 3 |
| π |
| 3 |
依题意知,
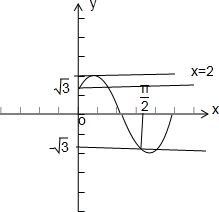
-
| 3 |
| 3 |
| 3 |
| 3 |
解得:0≤a<
| 3 |
2+
| ||
| 2 |
∴实数a的取值范围是{a|0≤a<
| 3 |
2+
| ||
| 2 |
故答案为:{a|0≤a<
| 3 |
2+
| ||
| 2 |
点评:本题考查三角恒等变换,着重考查正弦函数的单调性与最值,考查运算求解能力,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图,平面α⊥平面β,α∩β=直线l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∈直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )
如图,平面α⊥平面β,α∩β=直线l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∈直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )| A、当CD=2AB时,M,N两点不可能重合 |
| B、当AB,CD是异面直线时,直线MN可能与l平行 |
| C、当AB与CD相交,直线AC平行于l时,直线BD可以与l相交 |
| D、M,N两点可能重合,但此时直线AC与l不可能相交 |
已知向量
=2
-
,
=
+2
,
=
-
,
与
不共线,则不能构成基底的一组向量是( )
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| c |
| 1 |
| 2 |
| e1 |
| 3 |
| 2 |
| e2 |
| e1 |
| e2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=60米,并在点C测得塔顶A的仰角为60°,则塔高AB=
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=60米,并在点C测得塔顶A的仰角为60°,则塔高AB=