题目内容
设y=f(x)是R上的任意函数,下列叙述正确的是( )
| A、y=f(x)•f(-x)是奇函数 |
| B、y=f(x)•|f(-x)|是奇函数 |
| C、y=f(x)+f(-x)是偶函数 |
| D、y=f(x)-f(-x)是偶函数 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:由于函数的定义域都是R,故只看F(-x)与F(x)的关系,再根据奇函数、偶函数的定义作出判断.
解答:
解:在选项A中,设F(x)=f(x)f(-x),F(-x)=f(x)f(-x)=F(x),
故F(x)为偶函数,故A不正确.
在选项B中,f(x)|f(-x)|奇偶性不确定,故B不正确.
在选项C中,设F(x)=f(x)+f(-x),F(-x)=f(-x)+f(x)=F(x)是偶函数,故C正确.
在选项D中,F(x)=f(x)-f(-x),F(-x)=f(-x)-f(x)=-F(x),故为奇函数,故D不正确.
故选:C.
故F(x)为偶函数,故A不正确.
在选项B中,f(x)|f(-x)|奇偶性不确定,故B不正确.
在选项C中,设F(x)=f(x)+f(-x),F(-x)=f(-x)+f(x)=F(x)是偶函数,故C正确.
在选项D中,F(x)=f(x)-f(-x),F(-x)=f(-x)-f(x)=-F(x),故为奇函数,故D不正确.
故选:C.
点评:本题主要考查函数的奇偶性的判断方法,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知集合A={x|0<x<2},B={x|(x-1)(x+1)>0},则A∪B=( )
| A、(0,1) |
| B、(1,2) |
| C、(-∞,-1)∪(0,+∞) |
| D、(-∞,-1)∪(1,+∞) |
已知实数r是常数,如果M(x0,y0)是圆x2+y2=r2外的一点,那么直线x0x+y0y=r2与圆x2+y2=r2的位置关系是( )
| A、相交 | B、相切 |
| C、相离 | D、都有可能 |
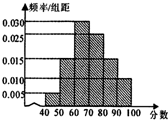 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为