题目内容
12.已知过定点P(-2,0)的直线l与曲线y=$\sqrt{2-{x}^{2}}$相交于A,B两点,O为坐标原点,当△AOB的面积最大值时,直线l的斜率为( )| A. | $\sqrt{3}$ | B. | 1 | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由曲线y=$\sqrt{2{-x}^{2}}$表示在x轴上方以及含与x轴的交点半圆,设出直线l的方程,利用△AOB的面积取最大值时,OA⊥OB,求出圆心O到直线l的距离d=1,从而求出直线的斜率k.
解答 解:由y=$\sqrt{2{-x}^{2}}$,得x2+y2=2(y≥0),
∴曲线y=$\sqrt{2{-x}^{2}}$表示圆x2+y2=2在x轴上方的部分(含与x轴的交点);
由题知,直线的斜率存在,设直线l的斜率为k(k>0),
则直线方程为y=k(x+2),即kx-y+2k=0,
当△AOB的面积取最大值时,OA⊥OB,
此时圆心O到直线l的距离d=1,如图所示;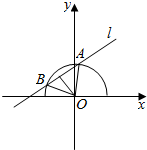
∴d=$\frac{|0-0+2k|}{\sqrt{{k}^{2}{+(-1)}^{2}}}$=1,
∴k=$\frac{\sqrt{3}}{3}$.
故选:C.
点评 本题考查了直线与圆的位置关系以及点到直线的距离公式的运用问题,解题的关键是根据△AOB的面积取到最大值时OA⊥OB,是中档题.

练习册系列答案
相关题目
12.设△ABC的外心P满足$\overrightarrow{AP}$=$\frac{2}{5}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),则cos∠BAC=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
9.下列定积分中,值等于零的是( )
| A. | ${∫}_{-1}^{2}$xdx | B. | ${∫}_{-1}^{1}$xsin2xdx | C. | ${∫}_{-1}^{1}$xsinxdx | D. | ${∫}_{-1}^{1}$x2sin2xdx |
2.若平面α的一个法向量为$\overrightarrow{n}$=(4,1,1),直线l的一个方向向量为$\overrightarrow{a}$=(-2,-3,3),则l与α所成角的正弦值为( )
| A. | $-\frac{{\sqrt{11}}}{11}$ | B. | $\frac{{\sqrt{11}}}{11}$ | C. | $\frac{{\sqrt{110}}}{11}$ | D. | $\frac{4\sqrt{11}}{33}$ |
 如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.
如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.