题目内容
12.设△ABC的外心P满足$\overrightarrow{AP}$=$\frac{2}{5}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),则cos∠BAC=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
分析 由外心在BC的中线AD上,可知△ABC是等腰三角形,根据$\overrightarrow{AP}$=$\frac{2}{5}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)得出AP与PD的关系.使用圆周角定理得出.
解答 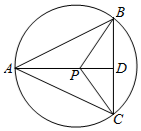 解:设BC中点为D,则$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}$,∴$\overrightarrow{AP}=\frac{4}{5}\overrightarrow{AD}$.∴AP=4PD.
解:设BC中点为D,则$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}$,∴$\overrightarrow{AP}=\frac{4}{5}\overrightarrow{AD}$.∴AP=4PD.
连结PB,PC,则PB=AP=PC,∴AD⊥BC,
∵∠BPD=∠BAC,∴cos∠BAC=cos∠BPD=$\frac{PD}{PB}$=$\frac{1}{4}$.
故选:C.
点评 本题考查了平面向量在几何中的应用,属于基础题.

练习册系列答案
相关题目
2.已知抛物线Γ:x2=-4y的焦点为F.直线(1+3λ)x-(1+λ)y+2=0过定点M.则|MF|的值为( )
| A. | 3 | B. | 2 | C. | $\sqrt{13}$ | D. | $\sqrt{17}$ |
12.已知过定点P(-2,0)的直线l与曲线y=$\sqrt{2-{x}^{2}}$相交于A,B两点,O为坐标原点,当△AOB的面积最大值时,直线l的斜率为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |