题目内容
已知函数f(x)=sinx+tanx.项数为27的等差数列{an}满足an∈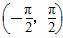 ,且公差d≠0.若f(a1)+f(a2)+…+f(a27)=0,则当k=________时,f(ak)=0.
,且公差d≠0.若f(a1)+f(a2)+…+f(a27)=0,则当k=________时,f(ak)=0.
14
[解析] ∵f(x)=sinx+tanx为奇函数,且在x=0处有定义,∴f(0)=0.
∵{an}为等差数列且d≠0,
∴an(1≤n≤27,n∈N*)对称分布在原点及原点两侧,
∵f(a1)+f(a2)+…+f(a27)=0,∴f(a14)=0.
∴k=14.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如表定义函数f(x):
| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 5 | 4 | 3 | 1 | 2 |
对于数列{an},a1=4,an=f(an-1),n=2,3,4,…,则a2014的值是( )
A.1 B.2 C.3 D.4
 =( )
=( )
 =a15
=a15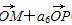 (直线MP不过点O),则S20等于( )
(直线MP不过点O),则S20等于( ) 的前100项和为( )
的前100项和为( ) B.
B. C.
C. D.
D.
 ,求出这个数列各项的值,使得这个数列中的每一项都是奇数,则a24+a25=________;研究发现,该数列中的奇数都会重复出现,那么第8个5是该数列的第________项.
,求出这个数列各项的值,使得这个数列中的每一项都是奇数,则a24+a25=________;研究发现,该数列中的奇数都会重复出现,那么第8个5是该数列的第________项.