题目内容
已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)(sin A-sin B)=(c-b)sin C,则△ABC面积的最大值为 .
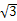 解析:把正弦定理a=2Rsin A,b=2Rsin B,c=2Rsin C代入已知得
解析:把正弦定理a=2Rsin A,b=2Rsin B,c=2Rsin C代入已知得
(2+b)(a-b)=(c-b)·c,
∴(2+b)(2-b)=(c-b)·c.
∴4-b2=c2-bc,∴b2+c2-bc=4.
∴cos A= =
= =
= .
.
∴A=60°.
又b2+c2=4+bc≥2bc,∴bc≤4.
∴S△ABC= bc·sin A=
bc·sin A= ×
×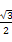 bc=
bc= bc≤
bc≤ ×4=
×4=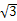 .
.
当且仅当b=c=2时取等号,故△ABC面积的最大值为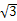 .
.

练习册系列答案
相关题目
 等于( )
等于( ) )的图象重合,则m+n的最小值为( )
)的图象重合,则m+n的最小值为( )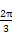 (B)
(B) (C)π (D)
(C)π (D)

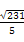 (B)
(B)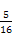 (C)
(C)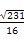 (D)
(D)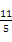
 ,求△ABC的面积.
,求△ABC的面积.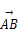 =a+2b,
=a+2b,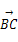 =-5a+6b,
=-5a+6b,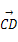 =7a-2b,则一定共线的三点是( )
=7a-2b,则一定共线的三点是( )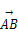 =(2,1),向量
=(2,1),向量 =(3,5),则向量
=(3,5),则向量 的坐标为 .
的坐标为 .  为边,
为边, 为对角线的矩形中,
为对角线的矩形中, ,
, ,则实数
,则实数 .
.