题目内容
将函数y=sin 2x(x∈R)的图象分别向左平移m(m>0)个单位,向右平移n(n>0)个单位,所得到的两个图象都与函数y=sin(2x+ )的图象重合,则m+n的最小值为( )
)的图象重合,则m+n的最小值为( )
(A)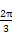 (B)
(B) (C)π (D)
(C)π (D)
C解析:利用图象变换的结论,函数y=sin2x(x∈R)的图象向左平移m(m>0)个单位,得函数y=sin[2(x+m)]=sin(2x+2m)的图象,向右平移n(n>0)个单位,得函数y=sin[2(x-n)]=sin(2x-2n)的图象,它们都与函数y=sin(2x+ )的图象重合,则最小的m,n应该为2m=
)的图象重合,则最小的m,n应该为2m= ,2π-2n=
,2π-2n= ,从而m+n=π.
,从而m+n=π.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 个单位长度
个单位长度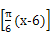 (x=1,2,3,…,12)来表示,已知6月份的平均气温最高,为28 ℃,12月份的平均气温最低,为18 ℃,则10月份的平均气温值为 ℃.
(x=1,2,3,…,12)来表示,已知6月份的平均气温最高,为28 ℃,12月份的平均气温最低,为18 ℃,则10月份的平均气温值为 ℃.  等于( )
等于( ) (C)-1 (D)1
(C)-1 (D)1 ,cos(α+β)=-
,cos(α+β)=- ,α∈(0,
,α∈(0, ),α+β∈(
),α+β∈(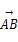 =(cos 18°,cos 72°),
=(cos 18°,cos 72°), =(2cos 63°,2cos 27°),则角B等于( )
=(2cos 63°,2cos 27°),则角B等于( ) (B)
(B) (C)
(C) (D)
(D)