题目内容
6.已知正方体ABCD-A1B1C1D1的一个面A1B1C1D1在半径为$\sqrt{3}$的半球底面上,A、B、C、D四个顶点都在此半球面上,则正方体ABCD-A1B1C1D1的体积为2$\sqrt{2}$.分析 如图所示,连接A1C1,B1D1,相交于点O.则点O为球心,OA=$\sqrt{3}$.设正方体的边长为x,则A1O=$\frac{\sqrt{2}}{2}$x.在Rt△OAA1中,由勾股定理解出x,即可得出.
解答  解:如图所示,
解:如图所示,
连接A1C1,B1D1,相交于点O.
则点O为球心,OA=$\sqrt{3}$.
设正方体的边长为x,则A1O=$\frac{\sqrt{2}}{2}$x.
在Rt△OAA1中,由勾股定理可得:$(\frac{\sqrt{2}}{2}x)^{2}$+x2=$(\sqrt{3})^{2}$,
解得x=$\sqrt{2}$.
∴正方体ABCD-A1B1C1D1的体积V=$(\sqrt{2})^{3}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查了正方体的性质与体积、球的性质、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知{an}为等差数列,a1+a3=2,则a2等于( )
| A. | -1 | B. | 1 | C. | 3 | D. | 7 |
18.如图,在长方体ABCD-A1B1C1D1中,AA1=2AB,AB=BC,则下列结论中正确的是( )
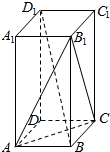

| A. | BD1∥B1C | B. | A1D1∥平面AB1C | C. | BD1⊥AC | D. | BD1⊥平面AB1C |
 如图,在直三棱柱ABC-A1B1C1中,已知A1C1⊥B1C1,CC1=2BC=2.
如图,在直三棱柱ABC-A1B1C1中,已知A1C1⊥B1C1,CC1=2BC=2.