题目内容

14．若函数$f（x）=\left\{\begin{array}{l}（a-1）x-2a，x＜2\\{log_a}x，x≥2\end{array}\right.$在R上单调递减，则实数a的取值范围是$[\frac{{\sqrt{2}}}{2}，1）$．

分析 根据题意，由函数的单调性的性质可得$\left\{\begin{array}{l}{a-1＜0}\\{0＜a＜1}\\{2（a-1）-2a≥lo{g}_{a}2}\end{array}\right.$，解可得a的取值范围，即可得答案．

解答 解：根据题意，函数$f（x）=\left\{\begin{array}{l}（a-1）x-2a，x＜2\\{log_a}x，x≥2\end{array}\right.$在R上单调递减，
必有$\left\{\begin{array}{l}{a-1＜0}\\{0＜a＜1}\\{2（a-1）-2a≥lo{g}_{a}2}\end{array}\right.$，化简可得$\left\{\begin{array}{l}{0＜a＜1}\\{lo{g}_{a}2≤-2}\end{array}\right.$，
解可得$\frac{\sqrt{2}}{2}$≤a＜1，
即a的取值范围是$[\frac{{\sqrt{2}}}{2}，1）$；
故答案为：$[\frac{{\sqrt{2}}}{2}，1）$．

点评 本题考查函数单调性的应用，关键是掌握函数单调性的定义．

练习册系列答案
相关题目
4．过抛物线y2=2px（p＞0）的焦点F作直线交抛物线于A，B，若S△OAF=4S△OBF，则直线AB的斜率为（　　）
A．±$\frac{3}{5}$B．±$\frac{4}{5}$C．±$\frac{3}{4}$D．±$\frac{4}{3}$
5．以下四个命题中，其中真命题的个数为（　　）
①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②对于命题p：?x∈R，使得x2+x+1＜0．则￢p：?x∈R，均匀x2+x+1≥0
③“x＜0”是“ln（x+1）＜0”的充分不必要条件；
④“若x+y=0，则x，y互为相反数”的逆命题．
A．1B．2C．3D．4
2．若0＜a＜2，0＜b＜2，则函数$f（x）=\frac{1}{3}{x^3}+\sqrt{a}{x^2}+2bx-3$存在极值的概率为$\frac{1}{4}$．
9．已知双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左、右焦点分别为F1，F2，P为双曲线C上的一点，若$|{\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}}|=\sqrt{{{|{\overrightarrow{P{F_1}}}|}^2}+{{|{\overrightarrow{P{F_2}}}|}^2}}$，$|{\overrightarrow{P{F_1}}}|=2|{\overrightarrow{P{F_2}}}|$，则双曲线C的离心率是$\sqrt{5}$．
19．已知直线a、b和平面β，有以下四个命题：
①若a∥β，a∥b，则b∥β；
②若a?β，b∩β=B，则a与b异面；
③若a⊥b，a⊥β，则b∥β；
④若a∥b，b⊥β，则a⊥β，
其中正确命题的个数是（　　）
A．0B．1C．2D．3
6．在区间[2，10]上任取一个数，这个数在区间[5，7]上的概率为（　　）
A．$\frac{1}{6}$B．$\frac{1}{4}$C．$\frac{1}{3}$D．$\frac{1}{2}$
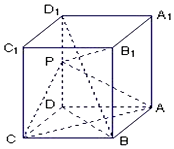3．如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P是DD1的中点．
求证：（1）直线BD1∥平面PAC
（2）①求异面直线PC与AA1所成的角．
②平面PAC⊥平面BDD1．
4．已知点P（-1，$\frac{3}{2}$）是椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上一点，F1，F2分别是椭圆E的左、右焦点，O是坐标原点，PF1⊥x轴．
（1）求椭圆E的方程；
（2）设A，B是椭圆E上两个动点，满足：$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ$\overrightarrow{PO}$（0＜λ＜4，且λ≠2），求直线AB的斜率．
（3）在（2）的条件下，当△PAB面积取得最大值时，求λ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网