题目内容
11．已知函数f（x）=（ax-1）ex，a∈R，e是自然对数底数．（Ⅰ）当a=1时，求函数f（x）的极值；
（Ⅱ）若函数f（x）在区间（0，1）上是单调增函数，求实数a的取值范围．
分析 （Ⅰ）求出函数f（x）的导数，解关于导函数的不等式，求出函数f（x）的单调区间，从而求出f（x）的极值即可；
（Ⅱ）问题转化为只要ax+a-1≥0对x∈（0，1）恒成立，分离参数得到$a≥\frac{1}{x+1}$对x∈（0，1]恒成立，根据函数的单调性求出a的范围即可．
解答 解：（Ⅰ）因为f'（x）=（ax+a-1）ex，
所以当a=1时，f'（x）=xex，
令f'（x）=0，解得x=0，
所以f（x），f'（x）的变化情况如下表：
| x | （-∞，0） | 0 | （0，+∞） |
| f'（x） | - | 0 | + |
| f（x） | 减 | 极小值 | 增 |
（Ⅱ）因为f（x）=（ax+a-1）ex，函数f（x）在区间（0，1）上是单调递增函数，
所以f'（x）≥0对x∈（0，1）恒成立，
又ex＞0，所以只要ax+a-1≥0对x∈（0，1）恒成立，
要使ax+a-1≥0对x∈（0，1）恒成立，
因为x＞0，所以$a≥\frac{1}{x+1}$对x∈（0，1]恒成立，
因为函数$g（x）=\frac{1}{x+1}$在（0，1）上单调递减，
只要$a≥g（0）=\frac{1}{0+1}=1$，所以a的取值范围是[1，+∞）．
点评 本题考查了函数的单调性、最值问题，考查导数的应用以及函数恒成立问题，是一道中档题．
练习册系列答案
相关题目
19．已知直线a、b和平面β，有以下四个命题：
①若a∥β，a∥b，则b∥β；
②若a?β，b∩β=B，则a与b异面；
③若a⊥b，a⊥β，则b∥β；
④若a∥b，b⊥β，则a⊥β，
其中正确命题的个数是（ ）
①若a∥β，a∥b，则b∥β；
②若a?β，b∩β=B，则a与b异面；
③若a⊥b，a⊥β，则b∥β；
④若a∥b，b⊥β，则a⊥β，
其中正确命题的个数是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
6．在区间[2，10]上任取一个数，这个数在区间[5，7]上的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
16．已知圆锥的表面积为6，且它的侧面展开图是一个半圆，则这个圆锥的底面半径为（ ）
| A． | $\sqrt{\frac{2}{π}}$ | B． | $\sqrt{\frac{1}{π}}$ | C． | $\sqrt{2π}$ | D． | $\sqrt{π}$ |
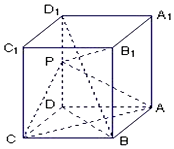如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P是DD1的中点．