题目内容
在△ABC中,内角A,B,C所对的边分别是a,b,c,且点(asinA,csinC)在直线x-y=(a-b)sinB上
(1)求角C的大小;
(2)若2cos2
-2sin2
=
,且A<B,求
.
(1)求角C的大小;
(2)若2cos2
| A |
| 2 |
| B |
| 2 |
| ||
| 3 |
| c |
| a |
考点:正弦定理,两角和与差的余弦函数,两角和与差的正弦函数
专题:计算题,解三角形
分析:(1)通过正弦定理化简表达式,利用余弦定理求出C的大小.
(2)由已知可得cosA+cosB=
,又C=
,有B=
-A,可得
cosA+
sinA=
,解得sinA=
±
,由正弦定理可求
=
的值.
(2)由已知可得cosA+cosB=
| ||
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
| c |
| a |
| sinC |
| sinA |
解答:
解:(1)∵点(asinA,csinC)在直线x-y=(a-b)sinB上,
∵asinA=(a-b)sinB+csinC,
由正弦定理
=
=
,得a2=(a-b)b+c2,
即a2+b2-c2=ab.①
由余弦定理得cosC=
=
,
结合0<C<π,得C=
.
(2)∵2cos2
-2sin2
=
,
∴cosA+cosB=
,
∵C=
,
∴B=
-A,
∵A<B,
∴A为锐角,
∴cosA+cos(
-A)=
cosA+
sinA=
,
∴可解得:12sin2A-12sinA+1=0,
∴解得:sinA=
±
,
∴由正弦定理可得:
=
=
=3
±3
.
∵asinA=(a-b)sinB+csinC,
由正弦定理
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
即a2+b2-c2=ab.①
由余弦定理得cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
结合0<C<π,得C=
| π |
| 3 |
(2)∵2cos2
| A |
| 2 |
| B |
| 2 |
| ||
| 3 |
∴cosA+cosB=
| ||
| 3 |
∵C=
| π |
| 3 |
∴B=
| 2π |
| 3 |
∵A<B,
∴A为锐角,
∴cosA+cos(
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
∴可解得:12sin2A-12sinA+1=0,
∴解得:sinA=
| 1 |
| 2 |
| ||
| 6 |
∴由正弦定理可得:
| c |
| a |
| sinC |
| sinA |
| ||||
|
| 3 |
| 2 |
点评:本题考查正弦定理与余弦定理的应用,考查分析问题解决问题的能力,考查了计算能力和转化思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}中,已知a1=1,对任意的k∈N*,有a2k-1,a2k,a2k+1成等比数列,且公比为2k,则a101的值为( )
| A、2 502 |
| B、250×51 |
| C、2 512 |
| D、2101×102 |
 若如图所示的程序框图输出的S是62,则在判断框中①表示的“条件”应该是( )
若如图所示的程序框图输出的S是62,则在判断框中①表示的“条件”应该是( )| A、n≤7 | B、n≤6 |
| C、n≤5 | D、n≤4 |
若函数y=2x图象上存在点(x,y)满足约束条件
,则实数m的最大值为( )
|
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
设Sn为等差数列{an}(n∈N+)的前n项和,且S2=S6,a4=1,则a5=( )
| A、-1 | B、0 | C、1 | D、2 |
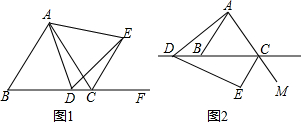 如图1所示,点D是等边三角形ABC的边BC上一点,连结AD作∠ADE=60°,交∠ABC的外角平分线CE于E
如图1所示,点D是等边三角形ABC的边BC上一点,连结AD作∠ADE=60°,交∠ABC的外角平分线CE于E