题目内容
设偶函数f(x)的定义域为R,当x∈[0,+∞)时f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是( )
| A、f(π)<f(-2)<f(-3) |
| B、f(π)<f(-3)<f(-2) |
| C、f(π)>f(-2)>f(-3) |
| D、f(π)>f(-3)>f(-2) |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系,进行判断即可.
解答:
解:∵f(x)是偶函数且当x∈[0,+∞)时f(x)是增函数,
∴f(π)>f(3)>f(2),
即f(π)>f(-3)>f(-2),
故选:D.
∴f(π)>f(3)>f(2),
即f(π)>f(-3)>f(-2),
故选:D.
点评:本题主要考查函数值的大小比较,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
过点A(0,2 ),B (2,0)的直线的斜率是( )
| A、2 | B、1 | C、-2 | D、-1 |
命题p的逆命题是真命题,则下列说法一定正确的是( )
| A、命题p为真命题 |
| B、命题p为假命题 |
| C、命题p的否命题为真命题 |
| D、命题p的逆否命题为真命题 |
命题“若α=
,则tanα=1”的否命题是( )
| π |
| 4 |
A、若α≠
| ||
B、若α=
| ||
C、若tanα≠1,则α≠
| ||
D、若tanα≠1,则α=
|
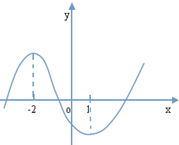
已知函数f(x)=ax3+bx2+cx+d的图象如图所示,其导函数是f′(x),则
=( )
| f′(3) |
| f′(-1) |

| A、-2 | B、2 | C、5 | D、-5 |