题目内容
已知a是锐角,求证:cos(sina)>sin(cosa).
考点:三角函数线
专题:三角函数的求值
分析:正弦函数、余弦函数的值域以及sina+cosa=
sin(a+
) )<
,可得cosa<
-sina,再两边同时取正弦证得结论.
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
解答:
证明:因为a是锐角,所以sina,cosa∈(0,1)⊆(0,
),
再有sina+cosa=
sin(a+
) )≤
<
,
所以cosa<
-sina,再两边同时取正弦可得:
sin(cosa)<sin(
-sina)=cos(sina),
即 cos(sina)>sin(cosa).
| π |
| 2 |
再有sina+cosa=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 2 |
所以cosa<
| π |
| 2 |
sin(cosa)<sin(
| π |
| 2 |
即 cos(sina)>sin(cosa).
点评:本题主要考查正弦函数、余弦函数的值域,正弦函数的单调性,属于基础题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
已知[x]表示不超过x的最大整数,设全集U=R,函数y=lg[x]+
的定义域为集合A,则∁UA=( )
| 1 | ||
|
| A、[1,2) |
| B、(-∞,1]∪(2,+∞) |
| C、(1,2] |
| D、(-∞,1)∪[2,+∞) |
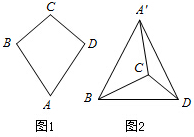 如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.
如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.