题目内容
（1+x）2n（n∈N*）的展开式中，系数最大的项是（ ）
A、第
| ||
| B、第n项 | ||
| C、第n+1项 | ||
| D、第n项与第n+1项 |
考点：二项式定理
专题：二项式定理
分析：由于第r+1项的系数为
，可得当r=n时，系数最大，从而得出结论．
| C | r 2n |
解答：
解：由于第r+1项的系数为
，故当r=n时，系数最大，即第n+1项的系数最大，
故选：C．
| C | r 2n |
故选：C．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，属于基础题．
练习册系列答案
相关题目
计算
cosxdx的结果是（ ）
| ∫ |
-
|
| A、4 | B、2 | C、0 | D、π |
（理科）已知-3＜a＜2，3＜b＜4，则
的取值范围为（ ）
| a |
| b |
A、（-1，
| ||||
B、（-
| ||||
C、（-1，
| ||||
D、（-
|
某学校有教师150人，其中高级教师15人，中级教师45人，初级教师90人．现按职称分层抽样选出30名教师参加教工代表大会，则选出的高、中、初级教师的人数分别为（ ）
| A、3，9，18 |
| B、5，10，15 |
| C、3，10，17 |
| D、5，9，16 |
已知y=f（x）是偶函数，而y=f（x+1）是奇函数，且对任意0≤x≤1，f（x）递减，都有f（x）≥0，则a=f（2010），b=f（
），c=-f（
）的大小关系是（ ）
| 5 |
| 4 |
| 1 |
| 2 |
| A、b＜c＜a |
| B、c＜b＜a |
| C、a＜c＜b |
| D、a＜b＜c |
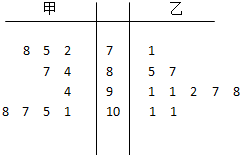两名射击运动员甲、乙在某次比赛中的成绩（单位：环）用茎叶图表示如图，甲、乙两人射击成绩的中位数分别用n甲、n乙表示，则（ ）| A、n甲＞n乙 |
| B、n甲＜n乙 |
| C、n甲=n乙 |
| D、n甲、n乙的大小关系不确定 |
今年4月20日8：30分四川芦山发生强地震，得知此消息，某医院决定从4名内科和6名外科医生（包含一名骨外科专家）10名医生中，用分层抽样的方式组成一个5人的医疗小组赶赴灾区展开震后的救护工作，则骨外科专家被选派的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f1（x）=sinx-cosx，fn+1（x）是fn（x）的导函数，即f2（x）=f1′（x），f3（x）=f2′（x），…，fn+1（x）=fn′（x），n∈N*，则f2013（x）=（ ）
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |