题目内容
执行如图所示的程序框图,则输出结果S的值为 .


考点:程序框图
专题:计算题,算法和程序框图
分析:算法的功能是求S=cos
+cos
+…+cos
的值,根据条件确定最后一次循环的n值,再利用余弦函数的周期性计算输出S的值.
| π |
| 3 |
| 2π |
| 3 |
| nπ |
| 3 |
解答:
解:由程序框图知:算法的功能是求S=cos
+cos
+…+cos
的值,
∵跳出循环的n值为2015,
∴输出S=cos
+cos
+…+cos
,
∵cos
+cos
+cos
+cos
+cos
+cos
=cos
+cos
+cos
-cos
-cos
-cos
=0,
∴S=cos
+cosπ=-
.
故答案为:-
.
| π |
| 3 |
| 2π |
| 3 |
| nπ |
| 3 |
∵跳出循环的n值为2015,
∴输出S=cos
| π |
| 3 |
| 2π |
| 3 |
| 2014π |
| 3 |
∵cos
| nπ |
| 3 |
| (n+1)π |
| 3 |
| (n+2)π |
| 3 |
| (n+3)π |
| 3 |
| (n+4)π |
| 3 |
| (n+5)π |
| 3 |
| nπ |
| 3 |
| (n+1)π |
| 3 |
| (n+2)π |
| 3 |
| nπ |
| 3 |
| (n+1)π |
| 3 |
| (n+2)π |
| 3 |
∴S=cos
| 2π |
| 3 |
| 3 |
| 2 |
故答案为:-
| 3 |
| 2 |
点评:本题考查了循环结构的程序框图,关键框图的流程判断算法的功能是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示的程序框图,程序运行时,若输入的S=-10,则输出的值为( )


| A、8 | B、9 | C、10 | D、11 |
设min{f(x),g(x)}=
,若函数h(x)=x2+px+q(p,q∈R)的图象经过不同的两点(α,0)、(β,0),且存在整数n,使得n<α<β<n+1成立,则( )
|
A、min{h(n),h(n+1)}>
| ||
B、min{h(n),h(n+1)}<
| ||
C、min{h(n),h(n+1)}=
| ||
D、min{h(n),h(n+1)}≥
|
角α终边上有一点(-1,2),则下列各点中在角2α的终边上的点是( )
| A、(3,4) |
| B、(-3,-4) |
| C、(4,3) |
| D、(-4,-3) |
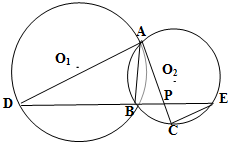 如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为
如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为