设A.B.C是空间任意三点.下列结论错误的是( )A．$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$B．$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=0C．$\overrightarrow{AB}$-$\overrightar 题目和参考答案——青夏教育精英家教网——

题目内容

4．设A，B，C是空间任意三点，下列结论错误的是（　　）

A．

$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$

B．

$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=0

C．

$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{CB}$

D．

$\overrightarrow{AB}$=-$\overrightarrow{BA}$

分析由空间向量的加，减法的法则可知$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$，$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$，$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{CB}$；由相反向量知$\overrightarrow{AB}$=-$\overrightarrow{BA}$．

解答解：由加法的三角形法则知，
$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$；
$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$；
由减法的三角形法则知，
$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{CB}$；
由相反向量知，$\overrightarrow{AB}$=-$\overrightarrow{BA}$；
故选：B．

点评本题考查了空间向量的加法、减法的法则应用．

练习册系列答案

英才教程探究习案课时精练系列答案

小学学习好帮手系列答案

初中语文阅读轻松组合周周练系列答案

小学同步三练核心密卷系列答案

剑桥小学英语系列答案

作业本江西教育出版社系列答案

新起点百分百单元测试卷系列答案

状元口算计算系列答案

题库精选系列答案

复习与测评单元综合测试卷系列答案

相关题目

14．设函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=2^x-3x+k（k为常数），则f（-1）=（　　）

15．数列{a_n}满足：a_n-1+a_n+1＞2a_n（n＞1，n∈N^*），给出下述命题：
①若数列{a_n}满足：a₂＞a₁，则a_n＞a_n-1（n＞1，n∈N^*）成立；
②存在常数c，使得a_n＞c（n∈N^*）成立；
③若p+q＞m+n（其中p，q，m，n∈N^*），则a_p+a_q＞a_m+a_n；
④存在常数d，使得a_n＞a₁+（n-1）d（n∈N^*）都成立．
上述命题正确的①④．（写出所有正确结论的序号）

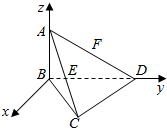如图点A（0，0，a），在四面体ABCD中，AB⊥平面BCD，BC=CD，∠BCD=90°，∠ADB=30°，E，F分别是AC，AD的中点，求D，C，E，F这四点的坐标．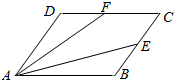

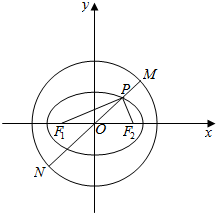19．平行四边形ABCD中，E、F分别是BC、CD的中点，记$\overrightarrow{AE}$=$\overrightarrow{a}$，$\overrightarrow{AF}$=$\overrightarrow{b}$，试用$\overrightarrow{a}$、$\overrightarrow{b}$表示向量$\overrightarrow{AB}$，$\overrightarrow{AD}$．

如图，已知椭圆C：$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1，圆O：x²+y²=13，椭圆C的左右焦点分别为F₁、F₂，过椭圆上一点P和原点O作直线l交圆O于M，N两点，若|PF₁|•|PF₂|=6，则|PM|•|PN|的值为（　　）

16．已知椭圆的中心在原点，一个焦点为F（3，0），若以其四个顶点为顶点的四边形的面积是40，则该椭圆的方程是$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$．

13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+y²=1（a＞1）的左焦点为F，上顶点为B．
（1）若直线FB的一个方向向量为（1，$\frac{\sqrt{3}}{3}$），求实数a的值；
（2）若a=$\sqrt{2}$，直线l：y=kx-2与椭圆C相交于M、N两点，且$\overrightarrow{FM}$•$\overrightarrow{FN}$=3，求实数k的值．

14．某班同学要安排学校晚会的3个音乐节目，2个舞蹈节目和1个曲艺节目的演出顺序，要求2个舞蹈节目不连排，曲艺节目不排首尾，则不同排法的种数为（　　）