题目内容
16.已知椭圆的中心在原点,一个焦点为F(3,0),若以其四个顶点为顶点的四边形的面积是40,则该椭圆的方程是$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$.分析 由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).可得$\left\{\begin{array}{l}{c=3}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{2}×2a×2b=40}\end{array}\right.$,解出即可得出.
解答 解:由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
∴$\left\{\begin{array}{l}{c=3}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{2}×2a×2b=40}\end{array}\right.$,解得c=3,a=5,b=4.
∴该椭圆的标准方程为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$.
故答案为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$.
点评 本题考查了椭圆的标准方程及其性质、四边形形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.运行程序框图,若输入x的值为1,则输出S的值为( )
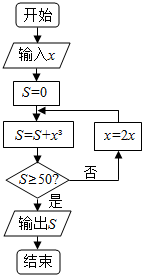

| A. | 64 | B. | 73 | C. | 512 | D. | 585 |
4.设A,B,C是空间任意三点,下列结论错误的是( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=0 | C. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{CB}$ | D. | $\overrightarrow{AB}$=-$\overrightarrow{BA}$ |
 如图,点E为△ABC中AB边的中点,点F为AC的三等分点(靠近点A),BF交CE于点G,若$\overrightarrow{AG}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x+y=$\frac{7}{5}$.
如图,点E为△ABC中AB边的中点,点F为AC的三等分点(靠近点A),BF交CE于点G,若$\overrightarrow{AG}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x+y=$\frac{7}{5}$.