题目内容
若两个非零向量
，
满足|
+
|=|
-
|=2|
|，则
+
与
-
的夹角为 ．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：如图所示，设
=
，
=
，由题意可得四边形ABCD是矩形，且
=
=cos∠BAC，求得∠BAC的值，可得∠OBA的值．再由三角形内角和公式求得∠COD的值，即为所求．
| AB |
| a |
| AD |
| b |
| AB |
| AC |
| 1 |
| 2 |
解答：
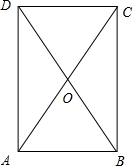解：如图所示，设
=
，
=
，∵两个非零向量满足|
+
|=|
-
|=2|
|，
∴四边形ABCD是矩形，且
=
=cos∠BAC，∴∠BAC=∠OAB=
，
∴∠OBA=
．∵∠COD=π-（∠OAB+∠OBA）=
．
再根据
+
与
-
的夹角为∠COD，
故答案为：
．
解：如图所示，设| AB |
| a |
| AD |
| b |
| a |
| b |
| a |
| b |
| a |
∴四边形ABCD是矩形，且
| AB |
| AC |
| 1 |
| 2 |
| π |
| 3 |
∴∠OBA=
| π |
| 3 |
| π |
| 3 |
再根据
| a |
| b |
| b |
| a |
故答案为：
| π |
| 3 |
点评：本题考查了向量的平行四边形法则和矩形的定义、直角三角形的边角关系，属于基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
