题目内容
如图，四边形ABCD是边长为1的正方形，延长CD至E，使得DE=2CD．动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，| AP |
| AB |
| AE |
| A、[-1，1] |
| B、[-1，2] |
| C、[-2，1] |
| D、[0，2] |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由题意，不妨设正方形的边长为1，建立如图所示的坐标系，则B（1，0），E（-2，1），
=λ
+μ
=λ（1，0）+μ（-2，1）=（λ-2μ，μ）．对于点P在四条边的位置分类讨论即可得出．
| AP |
| AB |
| AE |
解答：
解：由题意，不妨设正方形的边长为1，建立如图所示的坐标系，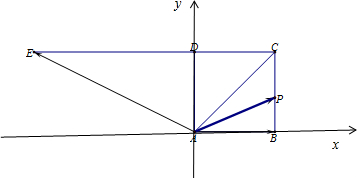
则B（1，0），E（-2，1），
=λ
+μ
=λ（1，0）+μ（-2，1）
=（λ-2μ，μ）．
当P∈AB时，有0≤λ-2μ≤1，μ=0，可得0≤λ≤1，故有0≤λ-μ≤1；
当P∈BC时，有λ-2μ=1，0≤μ≤1，
∴0≤λ-μ≤2；
当P∈CD时，有0≤λ-2μ≤1，μ=1，
∴1≤λ-μ≤2；
当P∈AD时，有λ-2μ=0，0≤μ≤1，∴0≤λ-μ≤1．
综上可得：0≤λ-μ≤2．
故选：D．
则B（1，0），E（-2，1），
| AP |
| AB |
| AE |
=（λ-2μ，μ）．
当P∈AB时，有0≤λ-2μ≤1，μ=0，可得0≤λ≤1，故有0≤λ-μ≤1；
当P∈BC时，有λ-2μ=1，0≤μ≤1，
∴0≤λ-μ≤2；
当P∈CD时，有0≤λ-2μ≤1，μ=1，
∴1≤λ-μ≤2；
当P∈AD时，有λ-2μ=0，0≤μ≤1，∴0≤λ-μ≤1．
综上可得：0≤λ-μ≤2．
故选：D．
点评：本题考查了向量的坐标运算、不等式的性质，考查了分类讨论的思想方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
若定义在R上的偶函数f（x）满足“对任意x1，x2∈（-∞，0），当x1-x2＜0时，都有f（x1）-f（x2）＜0”，则a=f（-2）与b=f（3）的大小关系为（ ）
| A、a＞b | B、a＜b |
| C、a=b | D、不确定 |
把函数y=
cosx-sinx的图象向右平移a个单位，所得图象关于y轴对称，则a的最大负值是（ ）
| 3 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
已知等差数列{an}的前n项和为Sn，且满足S3≤6，S4≥8，S6≤20，当a4取得最大值时，数列{an}的公差为（ ）
| A、4 | ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1（a＞0，b＞0）的离心率e=2，则
的最小值为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| a2+e |
| b |
A、
| ||||
B、
| ||||
C、2
| ||||
D、2
|
下列各组函数表示同一个函数的是（ ）
A、y=x+1与y=
| |||||||
B、y=x与y=
| |||||||
C、y=
| |||||||
D、y=
|
曲线x2+y2=|x|+|y|所围成的面积为（ ）
A、
| ||
| B、π+2 | ||
| C、2π+1 | ||
| D、均不对 |