题目内容
4.已知数列{an}满足:a1=-13,a6+a8=-2,且an-1=2an-an+1(n≥2),则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前13项和为( )| A. | $\frac{1}{13}$ | B. | -$\frac{1}{13}$ | C. | $\frac{1}{11}$ | D. | -$\frac{1}{11}$ |
分析 由条件可得an+1-an=an-an-1,可得数列{an}为等差数列,设公差为d,运用等差数列的通项公式解方程可得d,求得通项公式,以及$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-15)(2n-13)}$=$\frac{1}{2}$($\frac{1}{2n-15}$-$\frac{1}{2n-13}$),运用数列的求和方法:裂项相消求和,即可得到所求和.
解答 解:an-1=2an-an+1(n≥2),
可得an+1-an=an-an-1,
可得数列{an}为等差数列,设公差为d,
由a1=-13,a6+a8=-2,即为2a1+12d=-2,
解得d=2,
则an=a1+(n-1)d=2n-15.
$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-15)(2n-13)}$=$\frac{1}{2}$($\frac{1}{2n-15}$-$\frac{1}{2n-13}$),
即有数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前13项和为$\frac{1}{2}$($\frac{1}{-13}$-$\frac{1}{-11}$+$\frac{1}{-11}$-$\frac{1}{-9}$+…+$\frac{1}{11}$-$\frac{1}{13}$)
=$\frac{1}{2}$×(-$\frac{1}{13}$-$\frac{1}{13}$)=-$\frac{1}{13}$.
故选:B.
点评 本题考查等差数列的递推式和通项公式的运用,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
14. 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC上的点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1,$\overrightarrow{{E}_{n}B}$=(4an+3)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC上的点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1,$\overrightarrow{{E}_{n}B}$=(4an+3)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC上的点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1,$\overrightarrow{{E}_{n}B}$=(4an+3)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC上的点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1,$\overrightarrow{{E}_{n}B}$=(4an+3)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )| A. | 3•2n-1-2 | B. | 2n-1 | C. | 4n-2 | D. | 2•4n-1-1 |
15.在下列函数中,最小值为2的是( )
| A. | y=2x+2-x | B. | y=sinx+$\frac{1}{sinx}$(0<x<$\frac{π}{2}$) | ||
| C. | y=x+$\frac{1}{x}$ | D. | y=log3x+$\frac{1}{lo{g}_{3}x}$(1<x<3) |
16.设i是虚数单位,则复数z=$\frac{1+3i}{1-2i}$的共轭复数$\overline{z}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.已知复数z=$\frac{1+2i}{2}$(1+i)2(i为虚数单位),则z的共轭复数是( )
| A. | -2-i | B. | 2+3i | C. | $\frac{1}{2}$-i | D. | $\frac{1}{2}+i$ |
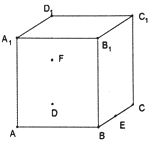 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,