题目内容
7.已知g(x)=mx+2,f(x)=x2-2x,若对?x1∈[-1,2].?x0∈[-1,2],有g(x1)=f(x0)成立,则m的取值范围是[-1,$\frac{1}{2}$].分析 由已知中f(x)=x2-2x,g(x)=mx+2,对?x1∈[-1,2],?x0∈[-1,2],使g(x1)=f(x0),可得函数g(x)=mx+2在区间[-1,2]上的值域是函数f(x)=x2-2x在区间[-1,2]上的值域的子集,由此可以构造关于m的不等式,解不等式即可求出m的取值范围.
解答 解:∵f(x)=x2-2x,
∴x0∈[-1,2],
∵f(x0)∈[-1,3]
又∵?x1∈[-1,2],?x0∈[-1,2],使g(x1)=f(x0),
若m>0,则g(-1)≥-1,g(2)≤3
解得-$\frac{1}{2}$≤m≤$\frac{1}{2}$,
即0<m≤$\frac{1}{2}$,
若m=0,则g(x)=2恒成立,满足条件;
若m<0,则g(-1)≤3,g(2)≥-1
解各m≥-1
即-1≤m<0
综上满足条件的m的取值范围是-1≤m≤$\frac{1}{2}$
故m的取值范围是[-1,$\frac{1}{2}$]
故答案为:[-1,$\frac{1}{2}$].
点评 本题考查的知识点是函数的值域,函数的定义域及其求法,二次函数的性质,其中根据已知条件对m进行分类讨论,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.若一个几何体的三视图如下图所示,则这个几何体是( )


| A. | 三棱锥 | B. | 四棱锥 | C. | 三棱柱 | D. | 四棱柱 |
19.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x-4y+3≥0}\\{x+y≥0}\\{x≥1}\end{array}\right.$,目标函数z=2x+y,则( )
| A. | z的最小值为3,z无最大值 | B. | z的最小值为1,最大值为3 | ||
| C. | z的最小值为3,z无最小值 | D. | z的最小值为1,z无最大值 |
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$与抛物线y2=4x的交点为A,B,且直线AB过双曲线与抛物线的公共焦点F,则双曲线的实轴长为( )
| A. | $\sqrt{2}$+1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$-1 | D. | 2$\sqrt{2}$-2 |
 是虚数单位,复数
是虚数单位,复数 ,则复数
,则复数 的虚部是( )
的虚部是( ) B.
B.
 D.2
D.2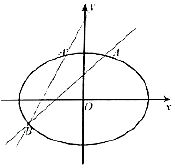 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({1,\frac{3}{2}})$,直线l:y=kx+1(k≠0)与椭圆E交于A,B两点,当k=1时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({1,\frac{3}{2}})$,直线l:y=kx+1(k≠0)与椭圆E交于A,B两点,当k=1时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.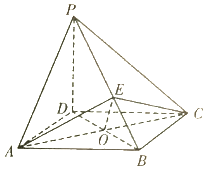 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是平行四边形,$∠BAD={60°},AB=2,PD=\sqrt{3},AD=BD$,O为AC与BD的交点,E为棱PB上一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是平行四边形,$∠BAD={60°},AB=2,PD=\sqrt{3},AD=BD$,O为AC与BD的交点,E为棱PB上一点. 如图,在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.
如图,在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.