题目内容
2.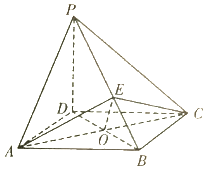 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是平行四边形,$∠BAD={60°},AB=2,PD=\sqrt{3},AD=BD$,O为AC与BD的交点,E为棱PB上一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是平行四边形,$∠BAD={60°},AB=2,PD=\sqrt{3},AD=BD$,O为AC与BD的交点,E为棱PB上一点.(1)证明:平面EAC⊥平面PBD;
(2)若PE=2EB,求二面角E-AC-B的大小.
分析 (1)证明AC⊥PD.AC⊥BD,推出AC⊥平面PBD,然后证明平面EAC⊥平面PBD.
(2)连接OE,说明∠EOB即为二面角E-AC-B的平面角,过E作EH∥PD,交BD于点H,则EH⊥BD,在RT△EHO中,求解二面角E-AC-B的大小即可.
解答 解:(1)∵PD⊥平面ABCD,AC?平面ABCD,∴AC⊥PD.
∵AD=BD,∠BAD=60°,∴△ABD为正三角形,四边形ABCD是菱形,
∴AC⊥BD,又PD∩BD=D,∴AC⊥平面PBD,
而AC?平面EAC,∴平面EAC⊥平面PBD.
(2)如图,连接OE,又(1)可知EO⊥AC,又AC⊥BD,
∴∠EOB即为二面角E-AC-B的平面角,
过E作EH∥PD,交BD于点H,则EH⊥BD,
又$PE=2EB,AB=2,PD=\sqrt{3},EH=\frac{{\sqrt{3}}}{3},OH=\frac{1}{3}$,
在RT△EHO中,$tan∠EOH=\frac{EH}{OH}=\sqrt{3}$,∴∠EOH=60°,
即二面角E-AC-B的大小为60°.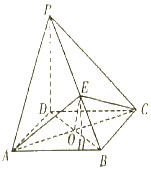
点评 本题考查直线与平面所成角的求法,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.将函数f(x)=$\sqrt{2}$sin2x-$\sqrt{2}$cos2x+1的图象向左平移$\frac{π}{4}$个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
| A. | 函数y=g(x)的最小正周期为π | |
| B. | 函数y=g(x)的图象的一条对称轴为直线x=$\frac{π}{8}$ | |
| C. | ${∫}_{0}^{\frac{π}{2}}$g(x)dx=$\sqrt{2}$ | |
| D. | 函数y=g(x)在区间[$\frac{π}{12}$,$\frac{5π}{8}$]上单调递减 |
14.设a>0,若关于x,y的不等式组$\left\{\begin{array}{l}{ax-y+2≥0}\\{x+y-2≥0}\\{x-2≤0}\end{array}\right.$,表示的可行域与圆(x-2)2+y2=9存在公共点,则z=x+2y的最大值的取值范围为( )
| A. | [8,10] | B. | (6,+∞) | C. | (6,8] | D. | [8,+∞) |
11.已知直线的方程是$\sqrt{3}x-y+1=0$,则直线的倾斜角是( )
| A. | 120° | B. | 150° | C. | 30° | D. | 60° |
12.已知双曲线$E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右顶点为A,抛物线C:y2=8ax的焦点为F.若在E的渐近线上存在点P,使得$\overrightarrow{AP}⊥\overrightarrow{FP}$,则E的离心率的取值范围是( )
| A. | (1,2) | B. | (1,$\frac{3\sqrt{2}}{4}$] | C. | $[{\frac{{3\sqrt{2}}}{4},+∞})$ | D. | (2,+∞) |
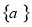 ,
, 为数列
为数列 的前
的前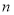 项和,若
项和,若 (
( ),记数列
),记数列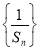 的前
的前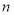 项和为
项和为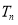 ,则
,则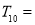 ( )
( )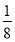 B.
B.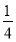
 D.
D.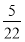
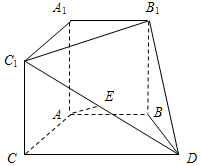 在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.
在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.