题目内容
14.设椭圆方程为x2+$\frac{y^2}{4}$=1,过点M(0,1)的直线L交椭圆于点A、B,O为坐标原点,点P满足$\overrightarrow{OP}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$,当L绕点M旋转时,求(1)当L的斜率为1时,求三角形ABC的面积;
(2)动点P的轨迹方程.
分析 (1)l:y=x+1,代入x2+$\frac{y^2}{4}$=1,求出A,B的坐标,即可求出三角形ABO的面积.
(2)设出直线l的方程,A,B的坐标,联立直线与椭圆的方程,利用韦达定理表示出x1+x2,利用直线方程表示出y1+y2,然后利用$\overrightarrow{OP}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$求得$\overrightarrow{OP}$的坐标,设出P的坐标,然后联立方程消去参数k求得x和y的关系式,P点轨迹可得.
解答 解:(1)l:y=x+1,代入x2+$\frac{y^2}{4}$=1,
整理得5x2+2x-3=0,∴x=-1或$\frac{3}{5}$
设A(x1,y1),B(x2,y2),则|x1-x2|=$\frac{8}{5}$,
∴三角形ABO的面积S=$\frac{1}{2}×1×\frac{8}{5}$=$\frac{4}{5}$;
(2)设P(x,y)是所求轨迹上的任一点,
①当斜率存在时,直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),
椭圆:4x2+y2-4=0
由直线l:y=kx+1代入椭圆方程得到:(4+k2)x2+2kx-3=0,
x1+x2=-$\frac{2k}{4+{k}^{2}}$,y1+y2=$\frac{8}{4+{k}^{2}}$,
由$\overrightarrow{OP}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$得:(x,y)=$\frac{1}{2}$(x1+x2,y1+y2),
即:x=-$\frac{k}{4+{k}^{2}}$,y=$\frac{4}{4+{k}^{2}}$
消去k得:4x2+y2-y=0
当斜率不存在时,AB的中点为坐标原点,也适合方程
所以动点P的轨迹方程为:4x2+y2-y=0.
点评 本小题主要考查平面向量的概念、直线方程的求法、椭圆的方程和性质等基础知识,以及轨迹的求法与应用、曲线与方程的关系等解析几何的基本思想和综合解题能力.

| A. | x+y-2=0 | B. | x-y+2=0 | C. | x+y+2=0 | D. | x-y-2=0 |
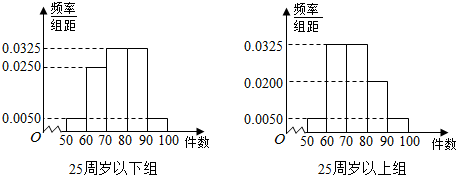
规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
附表:
| P(K2≥k) | 0.100 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |