题目内容
1．设点A（-3，5）和B（2，15），在直线l：3x-4y+4=0上找一点P，使|PA|+|PB|为最小，则这个最小值为5$\sqrt{13}$．分析 设点A（-3，5）关于直线l：3x-4y+4=0的对称点为A′（a，b），求出A′．可得|PA|+|PB|的最小值=|A′B|．
解答 解：设点A（-3，5）关于直线l：3x-4y+4=0的对称点为A′（a，b），
则$\left\{\begin{array}{l}{\frac{b-5}{a+3}×\frac{3}{4}=-1}\\{3×\frac{a-3}{2}-4×\frac{b+5}{2}+4=0}\end{array}\right.$，解得A′（3，-3）．
则|PA|+|PB|的最小值=|A′B|=5$\sqrt{13}$．
故答案为：5$\sqrt{13}$．
点评 本题考查了点关于直线对称点的求法、互相垂直的直线斜率之间的关系、中点坐标公式、两点之间的距离公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
13．函数$y={log_{\frac{1}{2}}}$（ax+2）在[-1，3]上递增，则a的取值范围是（ ）
| A． | （-∞，0） | B． | $（-\frac{2}{3}，0）$ | C． | （-1，0） | D． | （-3，-1） |
14．在等比数列，${S_n}={3^n}-1$，则a1等于（ ）
| A． | 2 | B． | 3 | C． | 6 | D． | 8 |
6．已知m，n为空间中两条不同的直线，α，β为空间中两个不同的平面，下列命题中正确的是（ ）
| A． | 若m∥α，m∥β，则α∥β | B． | 若m⊥α，m⊥n，则n∥α | C． | 若m∥α，m∥n，则n∥α | D． | 若m⊥α，m∥β，则α⊥β |
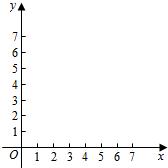已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x∈[1，4]}\\{（x-5）^{2}+1，x∈（4，7]}\end{array}\right.$．