题目内容
13.函数$y={log_{\frac{1}{2}}}$(ax+2)在[-1,3]上递增,则a的取值范围是( )| A. | (-∞,0) | B. | $(-\frac{2}{3},0)$ | C. | (-1,0) | D. | (-3,-1) |
分析 由条件利用复合函数的单调性,对数函数的定义域可得$\left\{\begin{array}{l}{a<0}\\{3a+2>0}\end{array}\right.$,由此求得a的范围.
解答 解:由函数$y={log_{\frac{1}{2}}}$(ax+2)在[-1,3]上递增,可得$\left\{\begin{array}{l}{a<0}\\{3a+2>0}\end{array}\right.$,
求得-$\frac{2}{3}$<a<0,
故选:B.
点评 本题主要考查复合函数的单调性,对数函数的定义域,属于基础题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
5.已知函数f(x)=2loga(x-1)(a>0且a≠1)恒过点(m,n),则在直角坐标系中,函数$g(x)={(\frac{1}{m+n})^{|{x+1}|}}$的大致图象为( )
| A. | 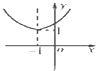 | B. | 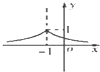 | C. | 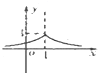 | D. | 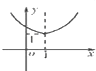 |
2.设z1、z2∈C,则“z1•z是实数”是“z1、z2互为共轭”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
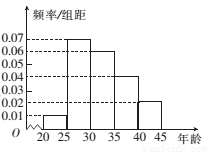
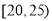 ,第2组
,第2组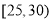 ,第3组
,第3组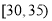 ,第4组
,第4组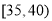 ,第5组
,第5组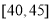 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.