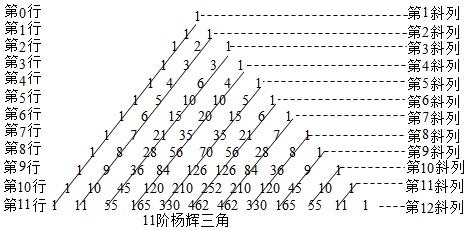
题目内容
13．已知数列{an}中，an=32，前n项和为Sn=63．（1）若数列{an}为公差为11的等差数列，求a1；
（2）若数列{an}为以a1=1为首项的等比数列，求数列{a${\;}_{n}^{2}$}的前m项和Tm．
分析 （1）通过联立$\frac{n（{a}_{1}+{a}_{n}）}{2}$=Sn=63、a1+11（n-1）=an=32，计算即得结论；
（2）通过联立a1qn-1=32、$\frac{{a}_{1}（1-{q}^{n}）}{1-q}$=63、a1=1，计算可知数列{an2}是首项为1、公比为4的等比数列，进而利用等比数列的求和公式计算即得结论．
解答 解：（1）由已知：$\frac{n（{a}_{1}+{a}_{n}）}{2}$=Sn=63，
a1+11（n-1）=an=32，
联立解得：a1=10，n=3或a1=1，n=$\frac{42}{11}$（舍）；
（2）由已知：a1qn-1=32且$\frac{{a}_{1}（1-{q}^{n}）}{1-q}$=63，
解得：q=2，n=6，
∴数列{an2}是首项为1、公比为4的等比数列，
∴Tm=$\frac{1-{4}^{m}}{1-4}$=$\frac{{4}^{m}-1}{3}$．
点评 本题考查数列的通项及前n项和，考查运算求解能力，注意解题方法的积累，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
10．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线与直线3x-4y-5=0垂直，则双曲线的离心率为（ ）
| A． | $\frac{5}{3}$或$\frac{5}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{5}{3}$ | D． | $\frac{5}{4}$ |
某校为了解全校高中学生五一小长假参加实践活动的情况，抽查了100名学生，统计他们假期参加实践活动的实践，绘成的频率分布直方图如图所示，这100名学生中参加实践活动时间在6-10小时内的人数为58．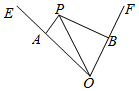
如图：有一人在∠EOF=60°的V型码头内位于P点的一艘船上，要想到达O地上岸，现有三种方案：