题目内容
5.函数f(x)=$\sqrt{lo{g}_{\frac{1}{2}}(x-1)-1}$的定义域为(0,$\frac{3}{2}$].分析 利用开偶次方被开方数非负列出不等式,然后求解即可.
解答 解:函数f(x)=$\sqrt{lo{g}_{\frac{1}{2}}(x-1)-1}$有意义,
可得:$lo{g}_{\frac{1}{2}}(x-1)-1≥0$,可得0$≤x-1≤\frac{1}{2}$,
解得1$<x≤\frac{3}{2}$.
函数的定义域为:(0,$\frac{3}{2}$].
故答案为:(0,$\frac{3}{2}$].
点评 本题考查函数的定义域的求法,对数不等式的解法,考查计算能力.

练习册系列答案
相关题目
13.已知空间四边形OABC,其对角线为AC,OB,且M,N分别是OA,BC的中点,G为MN的中点,则$\overrightarrow{OG}$等于( )
| A. | $\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{3}\overrightarrow{OB}$+$\frac{1}{3}\overrightarrow{OC}$ | B. | $\frac{1}{4}$($\overline{OA}+\overline{OB}+\overrightarrow{OC}$) | C. | $\frac{1}{3}$($\overline{OA}+\overline{OB}+\overrightarrow{OC}$) | D. | $\frac{1}{3}$$\overrightarrow{OA}+\frac{1}{6}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$ |
17.已知A={1,2,3,4},B={2,3,4,6},则A∩B=( )
| A. | {1,2} | B. | {2,3} | C. | {2,3,4} | D. | {1,2,3,4,6} |
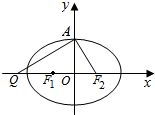 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交z轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}$+$\overrightarrow{{F_2}Q}$=$\overrightarrow{0}$,若过A,Q,F2三点的圆的半径为2.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交z轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}$+$\overrightarrow{{F_2}Q}$=$\overrightarrow{0}$,若过A,Q,F2三点的圆的半径为2.