题目内容
5.求形如函数y=f(x)g(x)(f(x)>0)的导数的方法可以为:先两边同取自然对数lny=g(x)lnf(x),再两边同时求导得到$\frac{1}{y}•{y^'}={g^'}(x)lnf(x)+g(x)•\frac{1}{f(x)}•{f^'}(x)$,于是得到y′,试用此法求的函数$y={x^{x^2}}$(x>0)的一个单调递增区间是( )| A. | (e,4) | B. | $(\frac{1}{{\sqrt{e}}},+∞)$ | C. | (0,e) | D. | $(0,\frac{1}{{\sqrt{e}}})$ |
分析 根据定义,先求原函数的导数,令导数大于0,解不等式即可.
解答 解:由题意得:
y′=f(x)g(x)[g′(x)lnf(x)+g(x)•$\frac{1}{f(x)}$•f′(x)]
=${x}^{{x}^{2}}$(2xlnx+x2•$\frac{1}{x}$)
=${x}^{{x}^{2}}$(2xlnx+x),
令y′>0,解得:x>$\frac{1}{\sqrt{e}}$,
故选:B.
点评 本题考查函数的单调性,要求首先读懂定义,并熟练掌握导数运算,同时要注意函数的定义域.属简单题.

练习册系列答案
相关题目
16.已知x,y满足约束条件$\left\{{\begin{array}{l}{3x-y≤0}\\{2y-3x-6≤0}\\ \begin{array}{l}x≥0\\ y≥0\end{array}\end{array}}\right.$,则$z=\frac{2^x}{{\sqrt{2^y}}}$的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | ${2^{-\frac{3}{2}}}$ |
13.已知$f(\sqrt{x})=x$,则函数f(x+2)为( )
| A. | y=x2+4x+4(x≥-2) | B. | y=x2-4x+4(x≥0) | C. | y=x2+2(x≥0) | D. | y=x2-2(x≥0) |
10.已知各项均为正数的等差数列{an},且a1+a7=20,a1•a7=64.
(I)求数列{an}的通项公式;
(Ⅱ)设bn=$\frac{{a}_{n}}{2×{4}^{n}}$,求数列的前n项和.
(I)求数列{an}的通项公式;
(Ⅱ)设bn=$\frac{{a}_{n}}{2×{4}^{n}}$,求数列的前n项和.
17.已知函数f(x)=sinωx+3sin(ωx+$\frac{π}{2}$)(ω>0)的最小正周期为π,则ω的值( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
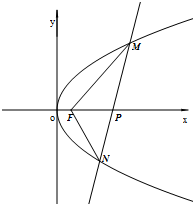 已知曲线C上任意一点到点F(1,0)的距离比到直线x+2=0的距离小1,点P(4,0).
已知曲线C上任意一点到点F(1,0)的距离比到直线x+2=0的距离小1,点P(4,0).