题目内容
不等式|2x-1|≥5的解为 .
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用
分析:本题为绝对值不等式,去绝对值是关键,可利用绝对值意义去绝对值,也可两边平方去绝对值.
解答:
解:∵|2x-1|≥5,
∴2x-1≥5或2x-1≤-5,
∴x≥3或x≤-2.
∴不等式的解集为{x|x≥3或x≤-2}.
故答案为:{x|x≥3或x≤-2}.
∴2x-1≥5或2x-1≤-5,
∴x≥3或x≤-2.
∴不等式的解集为{x|x≥3或x≤-2}.
故答案为:{x|x≥3或x≤-2}.
点评:本题主要考查解绝对值不等式,属基本题.解绝对值不等式的关键是去绝对值,去绝对值的方法主要有:利用绝对值的意义、讨论和平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个长方体,其正视图面积为
,侧视图面积为
,俯视图面积为
,则长方体的外接球的表面积为( )
| 6 |
| 3 |
| 2 |
| A、6π | ||
| B、24π | ||
C、6
| ||
D、
|
一个正八面体的八个顶点都在同一个球面上,如果该正八面体的棱长为
.则这个球的表面积为( )
| 2 |
| A、π | ||
| B、2π | ||
| C、4π | ||
D、
|
已知圆:C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y-1=0对称,则圆C2的方程为( )
| A、(x-2)2+(y-2)2=1 |
| B、(x+2)2+(y+2)2=1 |
| C、(x+2)2+(y-2)2=1 |
| D、(x-2)2+(y+2)2=1 |
执行如图所示的程序框图,输出的S值为( )


| A、162 | B、200 |
| C、242 | D、288 |
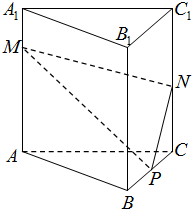 如图,在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥平面ABC,△ABC是边长为2的等边三角形,M是AA1上的一点,AA1=4,A1M=1.P是棱BC上的一点,且由点P沿棱柱侧面经过棱CC1到点M的最短距离为3
如图,在三棱柱ABC-A1B1C1中,已知侧棱AA1⊥平面ABC,△ABC是边长为2的等边三角形,M是AA1上的一点,AA1=4,A1M=1.P是棱BC上的一点,且由点P沿棱柱侧面经过棱CC1到点M的最短距离为3