题目内容
15.已知实数x,y满足条件$\left\{\begin{array}{l}x-y+5≥0\\ x+y≥0\\ x≤3\end{array}\right.$,z=x+yi(i为虚数单位),则|z-4+5i|的最小值等于$\sqrt{5}$.分析 作出不等式组对应的平面区域,根据复数的几何意义转化为两点间的距离进行求解即可.
解答 解:作出不等式组对应的平面区域如图,
|z-4+5i|的几何意义是复平面内区域内的点到点(4,-5)的距离,
由图象知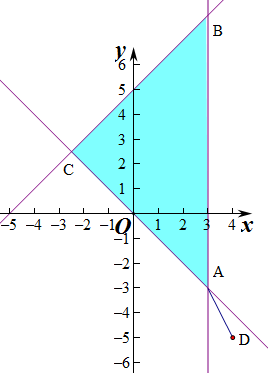 AD的距离最小,
AD的距离最小,
由$\left\{\begin{array}{l}{x=3}\\{x+y=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=-3}\end{array}\right.$,即A(3,-3),
则|z-4+5i|=$\sqrt{(3-4)^{2}+(-3+5)^{2}}$=$\sqrt{1+4}=\sqrt{5}$,
故答案为:$\sqrt{5}$.
点评 本题主要考查线性规划的应用,结合复数的几何意义转化为距离问题是解决本题的关键.

练习册系列答案
相关题目
6.下列四个结论中不正确的是( )
| A. | 若x>0,则x>sinx恒成立 | |
| B. | 命题“若x-sinx=0,则x=0”的否命题为“若x-sinx≠0,则x≠0” | |
| C. | “命题p∧q为真”是“命题p∨q为真”的充分不必要条件 | |
| D. | 命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0<0” |
10.已知α为第三象限角,化简cosα$\sqrt{\frac{1+sinα}{1-sinα}}$-sinα$\sqrt{\frac{1+cosα}{1-cosα}}$得( )
| A. | cosα-sinα | B. | sinα+cosα+2 | C. | sinα-cosα | D. | -sinα-cosα-2 |
20.已知函数f(x)=sin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的零点构成一个公差为$\frac{π}{2}$的等差数列,$f(0)=-\frac{{\sqrt{3}}}{2}$,则f(x)的一个单调递增区间是( )
| A. | $(-\frac{5π}{12},\frac{π}{12})$ | B. | $(-\frac{π}{6},\frac{π}{3})$ | C. | $(-\frac{π}{12},\frac{5π}{12})$ | D. | $(\frac{π}{12},\frac{7π}{12})$ |
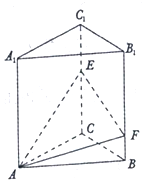 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.