题目内容
5.求下列函数的值域(1)y=$\frac{1{0}^{x}-1{0}^{-x}}{1{0}^{x}+1{0}^{-x}}$.
(2)y=4x+2x+1+1.
分析 (1)化简y=$\frac{1{0}^{x}-1{0}^{-x}}{1{0}^{x}+1{0}^{-x}}$=1-$\frac{2}{1{0}^{2x}+1}$,从而求值域;
(2)配方y=4x+2x+1+1=(2x)2+2•2x+1=(2x+1)2,从而求函数的值域.
解答 解:(1)y=$\frac{1{0}^{x}-1{0}^{-x}}{1{0}^{x}+1{0}^{-x}}$
=$\frac{1{0}^{2x}-1}{1{0}^{2x}+1}$=1-$\frac{2}{1{0}^{2x}+1}$,
∵102x>0,∴102x+1>1,
∴0<$\frac{2}{1{0}^{2x}+1}$<2,
∴-1<1-$\frac{2}{1{0}^{2x}+1}$<1,
故函数的值域为(-1,1).
(2)y=4x+2x+1+1=(2x)2+2•2x+1
=(2x+1)2,
∵2x>0,∴(2x+1)2>1,
故函数的值域为(1,+∞).
点评 本题考查了函数的值域的求法.

练习册系列答案
相关题目
16.若f(x)=0在区间(a,b)内恰有一解,则函数f(x)在区间(a,b)内( )
| A. | 单调递减 | B. | 单调递增 | ||
| C. | 单调递减或单调递增 | D. | 不能确定单调性 |
20.已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<0)的图象的相邻两个对称中心的坐标分别为($\frac{π}{9}$,0),($\frac{4π}{9}$,0),为了得到f(x)的图象,只需将g(x)=2sinωx的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{9}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{9}$个单位 |
14.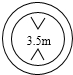 图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
 图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )| A. | h≤3.5 | B. | h≥3.5 | C. | h<3.5 | D. | h>3.5 |