题目内容
函数y=（
）
的递减区间为 ．
| 3 |
| 5 |
| -x2+x+2 |
考点：复合函数的单调性
专题：函数的性质及应用
分析：令t=-x2+x+2≥0，求得函数的定义域为[-1，2]，再根据y=(
)
，本题即求函数t在定义域内的增区间．再利用二次函数的性质可得结论．
| 3 |
| 5 |
| t |
解答：
解：令t=-x2+x+2≥0，求得x∈[-1，2]，故函数的定义域为[-1，2]，y=(
)
，
本题即求函数t在定义域内的增区间．
再利用二次函数的性质可得t=-x2+x+2=-(x-
)2+
的单调增区间为 [-1，
]，
故答案为：[-1，
]．
| 3 |
| 5 |
| t |
本题即求函数t在定义域内的增区间．
再利用二次函数的性质可得t=-x2+x+2=-(x-
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
故答案为：[-1，
| 1 |
| 2 |
点评：本题主要考查复合函数的单调性，指数函数、二次函数的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知直线l：Ax+By+C=0（A≠0，B≠0），点M0（x0，y0），则方程
=
表示（ ）
| x-x0 |
| A |
| y-y0 |
| B |
| A、经过点M0且平行于l的直线 |
| B、经过点M0且垂直于l的直线 |
| C、不一定经过M0但平行于l的直线 |
| D、不一定经过M0但垂直于l的直线 |
已知集合A={x|x-1＞0}，B={x||x-1|≤2}，则A∩B=（ ）
| A、{x|x≥1} |
| B、{x|-1≤x≤3} |
| C、{x|x≤3} |
| D、{x|1＜x≤3} |
设全集U={x|log2x＜3}，A={x|1＜2x＜32}，则CUA=（ ）
| A、（-∞，0]∪[5，8） |
| B、（-∞，0]∪（5，8） |
| C、[5，8） |
| D、（5，8） |
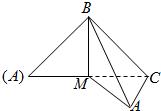如图，等腰直角△ABC中，已知AB=BC=2，M为AC中点，沿BM将它折成二面角，折后A，C间的距离为
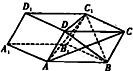已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2