题目内容
已知函数f（x）=
，若f（x）≤a|x|对任意实数x都成立，则实数a的最小值为 ．
|
考点：函数恒成立问题
专题：函数的性质及应用,不等式的解法及应用
分析：按照分段函数y=f（x）的表达式，分x=0，x＜0与x＞0三类讨论，分别求得a的最小值，取交即可．
解答：
解：若x=0，f（x）≤a|x|?0≤0对任意实数a都成立；
若x＜0，则f（x）≤a|x|?a≥
=
=x+4，
由于x＜0时，x+4＜4，所以a≥4；
若x＞0，则f（x）≤a|x|?a≥
=
，
令h（x）=
（x＞0），则h′（x）=
，
当0＜x＜e时，h′（x）＞0，
当x＞e时，h′（x）＜0，
所以，当x=e时，h（x）=
（x＞0）取得极大值，也是最大值，即h（x）max=h（e）=
，
所以，a≥
．
综上述，实数a的最小值为
．
故答案为：
．
若x＜0，则f（x）≤a|x|?a≥
| -x2-4x |
| |x| |
| -x2-4x |
| -x |
由于x＜0时，x+4＜4，所以a≥4；
若x＞0，则f（x）≤a|x|?a≥
| lnx |
| |x| |
| lnx |
| x |
令h（x）=
| lnx |
| x |
| 1-lnx |
| x2 |
当0＜x＜e时，h′（x）＞0，
当x＞e时，h′（x）＜0，
所以，当x=e时，h（x）=
| lnx |
| x |
| 1 |
| e |
所以，a≥
| 1 |
| e |
综上述，实数a的最小值为
| 1 |
| e |
故答案为：
| 1 |
| e |
点评：本题考查分段函数的应用，着重考查函数恒成立问题，考查分类讨论与等价转化思想，考查运算求解能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
在各项均为正数的等比数列{an}中，若a5a6=27，则log3a1+log3a2+…+log3a10=（ ）
| A、12 |
| B、10 |
| C、15 |
| D、27log35 |
设全集U={x|log2x＜3}，A={x|1＜2x＜32}，则CUA=（ ）
| A、（-∞，0]∪[5，8） |
| B、（-∞，0]∪（5，8） |
| C、[5，8） |
| D、（5，8） |
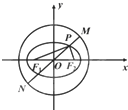如图，已知椭圆C：
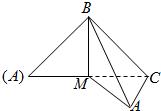如图，等腰直角△ABC中，已知AB=BC=2，M为AC中点，沿BM将它折成二面角，折后A，C间的距离为