题目内容
求直线l:2x-y-2=0,被圆C:(x-3)2+y2=9所截得的弦长.
考点:直线与圆的位置关系
专题:直线与圆
分析:算出已知圆的圆心为C(3,0),半径r=3.利用点到直线的距离公式,算出点C到直线直线l的距离d,由垂径定理加以计算,可得直线l被圆截得的弦长.
解答:
解:圆(x-3)2+y2=9的圆心为C(3,0),半径r=9,
∵点C到直线直线l:2x-y-2=0的距离d=
=
,
∴根据垂径定理,得直线l:2x-y-2=0被圆(x-3)2+y2=9截得的弦长为:
l=2
=2
=
.
∵点C到直线直线l:2x-y-2=0的距离d=
| |2×3-0-2| | ||
|
4
| ||
| 5 |
∴根据垂径定理,得直线l:2x-y-2=0被圆(x-3)2+y2=9截得的弦长为:
l=2
| r2-d2 |
32-(
|
2
| ||
| 5 |
点评:本题给出直线与圆的方程,求直线被圆截得的弦长,着重考查点到直线的距离公式、圆的方程和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知直线l:Ax+By+C=0(A≠0,B≠0),点M0(x0,y0),则方程
=
表示( )
| x-x0 |
| A |
| y-y0 |
| B |
| A、经过点M0且平行于l的直线 |
| B、经过点M0且垂直于l的直线 |
| C、不一定经过M0但平行于l的直线 |
| D、不一定经过M0但垂直于l的直线 |
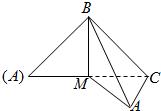 如图,等腰直角△ABC中,已知AB=BC=2,M为AC中点,沿BM将它折成二面角,折后A,C间的距离为
如图,等腰直角△ABC中,已知AB=BC=2,M为AC中点,沿BM将它折成二面角,折后A,C间的距离为 如图是正四面体的平面展开图,M、N、G分别为DE、BE、FE的中点,则在这个正四面体中,MN与CG所成角的大小为
如图是正四面体的平面展开图,M、N、G分别为DE、BE、FE的中点,则在这个正四面体中,MN与CG所成角的大小为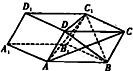 已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2
已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2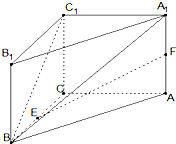 在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.
在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.