题目内容
1.设函数f(x)=k•ax-a-x(a>0且a≠1)是奇函数.(1)求常数k的值;
(2)设a>1,试判断函数y=f(x)在R上的单调性,并解关于x的不等式f(x2)+f(2x-1)<0.
分析 (1)可看出f(x)的定义域为R,而f(x)又是奇函数,从而有f(0)=0,这样可求出k=1;
(2)f(x)=ax-a-x,根据单调性的定义,设任意的x1,x2∈R,且x1<x2,然后作差,通分,提取公因式,便可说明f(x1)<f(x2),这便得出f(x)在R上单调递增,从而根据f(x)为奇函数和增函数便可由原不等式得到x2<1-2x,解该不等式便可得出原不等式的解集.
解答 解:(1)函数f(x)的定义域为R,f(x)是奇函数;
∴f(0)=k-1=0;
∴k=1;
(2)由(1),f(x)=ax-a-x,设x1,x2∈R,且x1<x2,则:
$f({x_1})-f({x_2})=({a^{x_1}}-{a^{-{x_1}}})-({a^{x_2}}-{a^{-{x_2}}})=({a^{x_1}}-{a^{x_2}})({1+\frac{1}{{{a^{{x_1}+{x_2}}}}}})$;
∵a>1,x1<x2;
${a^{x_1}}-{a^{x_2}}<0$,又$1+\frac{1}{{{a^{{x_1}+{x_2}}}}}>0$;
∴f(x1)-f(x2)<0;
即f(x1)<f(x2);
∴函数f(x)在R上是单调递增函数;
由f(x2)+f(2x-1)<0,得f(x2)<-f(2x-1);
即f(x2)<f(1-2x);
f(x)在R上单调递增;
∴x2<1-2x,即x2+2x-1<0;
解得$-1-\sqrt{2}<x<-1+\sqrt{2}$;
∴原不等式的解为$(-1-\sqrt{2},-1+\sqrt{2})$.
点评 考查奇函数的定义,奇函数在原点有定义时,原点处的函数值为0,函数单调性的定义,以及根据单调性定义判断一个函数单调性的方法和过程,根据函数单调性解不等式的方法.

 名校课堂系列答案
名校课堂系列答案| 直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
| 件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为X,并根据以下不等式进行评判(p表示相应事件的频率):①p(μ-σ<X≤μ+σ)≥0.6826.②P(μ-σ<X≤μ+2σ)≥0.9544③P(μ-3σ<X≤μ+3σ)≥0.9974.评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断设备M的性能等级.
(2)将直径小于等于μ-2σ或直径大于μ+2σ的零件认为是次品
(i)从设备M的生产流水线上随意抽取2件零件,计算其中次品个数Y的数学期望EY;
(ii)从样本中随意抽取2件零件,计算其中次品个数Z的数学期望EZ.
| A. | 1 | B. | 2 | C. | 4 | D. | 1或2 |
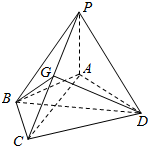 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,G为线段PC上的点,∠ABC=120°
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,G为线段PC上的点,∠ABC=120°