题目内容
直线y=
x+3与双曲线
-
=1的交点个数是（ ）
| b |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
| A、1 | B、2 | C、1或2 | D、0 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：求出双曲线的渐近线方程，然后判断直线与双曲线的交点个数即可．
解答：
解：双曲线
-
=1的渐近线方程为：y=±
x，因为直线y=
x+3与双曲线
-
=1的一条渐近线平行，
在y轴上的焦距为3，所以直线y=
x+3与双曲线
-
=1的交点个数是：1．
故选：A．
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| b |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
在y轴上的焦距为3，所以直线y=
| b |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
故选：A．
点评：本题考查双曲线方程的简单性质，考查基本知识的应用．
练习册系列答案
名校课堂系列答案
相关题目
如图，抛物线y=-x2+bx+c交x轴于A、B两点，交y轴于点C，直线y=x交抛物线y=-x2+bx+c对称轴右侧的抛物线于点P，连接PA、PC，设△AOP的面积为S1，△COP的面积为S2．正方体ABCD-A′B′C′D′中，异面直线AB′和A′D所成角为（ ）
| A、45° | B、60° |
| C、90° | D、60°或120° |
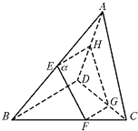如图，空间四边形ABCD中，E、F、G分别是AB、BC、CD上，且满足AE：EB=CF：FB=2：1，CG：GD=3：1，过E、F、G的平面交AD于点H．