题目内容
在等腰直角三角形中,过直角顶点C在直角内随机作射线CM交斜边AB于点M,则概率P(AM>AC)=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|
考点:几何概型
专题:概率与统计
分析:欲求AM的长大于AC的长的概率,先求出M点可能在的位置的长度,利用几何概型的概率公式即可得到结论.
解答:
解:在等腰直角三角形ABC中,设AC长为1,则AB长为
,
在AB上取点D,使AD=1,则若M点在线段DB上,满足条件AM>AC.
则M位于BD上,则|DB|=
-1,|AB|=
,
∴AM的长大于AC的长的概率为
=1-
,
故选:D
| 2 |
在AB上取点D,使AD=1,则若M点在线段DB上,满足条件AM>AC.

则M位于BD上,则|DB|=
| 2 |
| 2 |
∴AM的长大于AC的长的概率为
| ||
|
| ||
| 2 |
故选:D
点评:本题主要考查几何概型的概率的计算,求出满足条件的M的位置是解决本题的关键.

练习册系列答案
相关题目
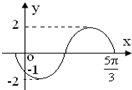 已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<π)图象的一部分(如图所示),则ω与φ的值分别为( )
已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<π)图象的一部分(如图所示),则ω与φ的值分别为( )A、
| ||||
B、1,-
| ||||
C、
| ||||
D、
|
椭圆
+y2=1的焦距比短轴长( )
| x2 |
| 10 |
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |
等差数列的相邻4项分别是a+1,a+3,b,a+b,那么a,b的值依次为( )
| A、2,7 | B、1,6 |
| C、0,5 | D、无法确定 |
阅读如图的程序框图,若运行相应的程序,则输出的S的值为( )

| A、64 | B、66 | C、98 | D、258 |
已知f(x)=ln(
-3x)+1,则f(lg3)+f(lg
)等于( )
| 1+9x2 |
| 1 |
| 3 |
| A、2 | B、1 | C、0 | D、-1 |
已知等差数列{an}的前n项和为Sn,且满足S4+a25=5,则一定有( )
| A、a6是常数 |
| B、S7是常数 |
| C、a13是常数 |
| D、S13是常数 |
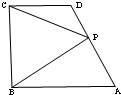 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设