题目内容

已知：△ABC的三边长分别为a=3，b=3
7
，c=6，则三角形中的最大的角为
 
．
考点：余弦定理
专题：解三角形
分析：利用余弦定理表示出cosB，把三边长代入求出B的度数即可．
解答： 解：∵ABC的三边长分别为a=3，b=3
7
，c=6，
∴cosB=
a2+c2-b2
2ac
=
9+36-63
36
=-
1
2
，
则B=120°．
故答案为：120°
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
已知角α的终边与单位圆的交点坐标为（-
1
2
，
3
2
），则cos2α=
 
．
函数y=
1-(
1
2
)x
的定义域是（　　）
A、[1，+∞）
B、（-∞，1]
C、[0，+∞）
D、（-∞，0]
求函数y=
log
1
2
sinx-1
的增区间．
将函数y=sin
π
2
x的图象向右平移2个单位后，得到函数f（x）的图象，则函数f（x）的单调递减区间是（　　）
A、[-1+2k，1+2k]，k∈Z
B、[1+4k，3+4k]，k∈Z
C、[-1+4k，1+4k]，k∈Z
D、[-1+4k+
4
π
，1+4k+
4
π
]，k∈Z
判断下列函数的奇偶性：
（1）f（x）=-3x+1；
（2）f（x）=-3x2+2．
已知M=[0，1]，N=[0，1]，则如图能表示M到N的映射的有
 
．
已知命题：
①若a≤b，则ac2≤bc2；
②“设a，b∈R，若a+b≠6，则a≠3或b≠3”是一个真命题；
③在△ABC中，cos2A＜cos2B的充要条件是A＞B；
④“所有的素数都是偶数”的否定是“所有的素数不都是偶数”；
⑤“P∨Q为真命题”是“￢P为假命题”的必要不充分条件．
其中正确命题的序号是
 
．
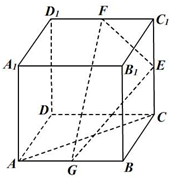如图，棱长为2的正方体ABCD-A1B1C1D1中，点E，F，G分别为棱CC1，C1D1，AB的中点．
（Ⅰ）求异面直线AC与FG所成角的大小；
（Ⅱ）求证：AC∥平面EFG．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网