题目内容
已知等比数列{an}的前n项和为Sn,a4-a1=78,S3=39,设bn=log3an,那么数列{bn}的前10项和为( )
| A、log371 | ||
B、
| ||
| C、50 | ||
| D、55 |
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:设出等比数列的公比,由已知列式求出等比数列的首项和公比,得到等比数列的通项公式,代入bn=log3an求得数列{bn}的通项,然后由等差数列的前n项和得答案.
解答:
解:设等比数列{an}的公比为q,
由a4-a1=78,S3=39,得
,
两式作比得:q-1=2,即q=3.
∴a1(33-1)=78,则a1=3.
∴an=a1qn-1=3•3n-1=3n.
∴bn=log3an=log33n=n.
则数列{bn}的前10项和S10=1+2+3+…+10=
=55.
故选:D.
由a4-a1=78,S3=39,得
|
两式作比得:q-1=2,即q=3.
∴a1(33-1)=78,则a1=3.
∴an=a1qn-1=3•3n-1=3n.
∴bn=log3an=log33n=n.
则数列{bn}的前10项和S10=1+2+3+…+10=
| (1+10)×10 |
| 2 |
故选:D.
点评:本题考查了等比数列的通项公式,考查了等差数列的前n项和,是基础的计算题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
执行如图所示的程序框图,若f(x)=3x2-1,取?=
,则输出的值为( )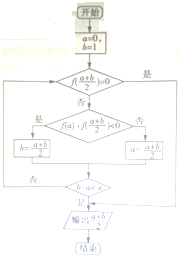
| 1 |
| 10 |

A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=ln
的图象大致为( )
| 1 |
| |2x-3| |
A、 |
B、 |
C、 |
D、 |
命题“?x∈R,cosx≤
”的否定是( )
| 1 |
| 2 |
A、?x∈R,cosx≥
| ||
B、?x∈R,cosx>
| ||
C、?∈R,cosx≥
| ||
D、?x∈R,cosx>
|
