题目内容
已知函数f(x)=
(Ⅰ)用定义法证明其在(2,+∞)上的单调性.
(Ⅱ)求f(x)在[4,5]上最值.
| 2 |
| x-2 |
(Ⅰ)用定义法证明其在(2,+∞)上的单调性.
(Ⅱ)求f(x)在[4,5]上最值.
考点:函数单调性的性质,函数单调性的判断与证明
专题:函数的性质及应用
分析:(Ⅰ)利用函数单调性的定义即可证明函数在(2,+∞)上的单调性.
(Ⅱ)根据函数的单调性和最值之间的关系即可得到结论.
(Ⅱ)根据函数的单调性和最值之间的关系即可得到结论.
解答:
(Ⅰ)证明、设x1,x2是(2,+∞)上任意两个值,且x1<x2,
∴f(x1)-f(x2)=
-
=
,
∵x1,x2∈(2,+∞)且x1<x2,
∴x1-x2<0,x1-2>0,x2-2>0,
∴f(x1)-f(x2)>0,
即f(x1)>f(x2)
∴函数f(x)=
在(2,+∞)上是减函数
(Ⅱ)解:由(Ⅰ)可知,函数f(x)在[4,5]上单调递减,
则f(x)min=f(5)=
=
;f(x)max=f(4)=
=1.
∴f(x1)-f(x2)=
| 2 |
| x1-2 |
| 2 |
| x2-2 |
| 2(x2-x1) |
| (x1-2)(x2-2) |
∵x1,x2∈(2,+∞)且x1<x2,
∴x1-x2<0,x1-2>0,x2-2>0,
∴f(x1)-f(x2)>0,
即f(x1)>f(x2)
∴函数f(x)=
| 2 |
| x-2 |
(Ⅱ)解:由(Ⅰ)可知,函数f(x)在[4,5]上单调递减,
则f(x)min=f(5)=
| 2 |
| 5-2 |
| 2 |
| 3 |
| 2 |
| 4-2 |
点评:本题主要考查函数单调性的证明以及函数最值的求解,利用单调性的定义是解决本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知x>4,则f(x)=
有( )
| x2-4x+1 |
| x-4 |
| A、最大值-6 | B、最小值6 |
| C、最大值-2 | D、最小值2 |
函数y=(
)x+1的图象必经过点( )
| 1 |
| 2 |
| A、(0,2) |
| B、(0,1) |
| C、(-1,0) |
| D、(1,0) |
在下列函数中,奇函数是( )
| A、f(x)=1-x2 |
| B、f(x)=x3 |
| C、f(x)=2x |
| D、f(x)=x+1 |
在复平面内,复数z=1-i对应于点P,则该点在以原点为极点,实轴的正半轴为极轴的极坐标系中所对应的极坐标是( )
A、(
| ||||
B、(2,
| ||||
C、(
| ||||
D、(2,
|
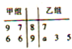 如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩,乙组记录中有一个数据模糊,无法确认,在图中以a表示,已知甲、乙两小组的数学成绩的平均分相同,则a=