题目内容
8．若$f（x）=\left\{{\begin{array}{l}{sin\frac{πx}{6}（x≤0）}\\{1-2x（x＞0）}\end{array}}\right.$，则f[f（1）]=-$\frac{1}{2}$．分析 利用分段函数先求出f（1）=1-2×1=-1，从而f[f（1）]=f（-1），由此能求出结果．
解答 解：∵$f（x）=\left\{{\begin{array}{l}{sin\frac{πx}{6}（x≤0）}\\{1-2x（x＞0）}\end{array}}\right.$，
∴f（1）=1-2×1=-1，
f[f（1）]=f（-1）=$sin（-\frac{π}{6}）$=-sin$\frac{π}{6}$=-$\frac{1}{2}$．
故答案为：-$\frac{1}{2}$．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
18．若x，y∈R，则“|x|＞|y|”是“x2＞y2”的（ ）
| A． | 充要条件 | B． | 充分而不必要条件 | ||
| C． | 必要而不充分条件 | D． | 既不充分也不必要条件 |
3．
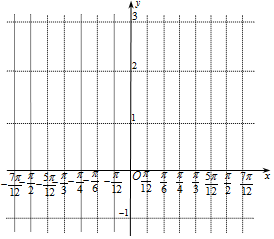某同学用“五点法”画函数$f（x）=2sin（2x-\frac{π}{3}）+1$在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上的图象时，列表并填入了部分数据，如表：
（1）请将上表数据补充完整，并在给出的直角坐标系中，画出f（x）在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上的图象；
（2）求f（x）的最小值及取最小值时x的集合；
（3）求f（x）在$x∈[0，\frac{π}{2}]$时的值域．
某同学用“五点法”画函数$f（x）=2sin（2x-\frac{π}{3}）+1$在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上的图象时，列表并填入了部分数据，如表：| 2x-$\frac{π}{3}$ | -$\frac{4}{3}$π | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2}{3}$π |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f（x） |
（2）求f（x）的最小值及取最小值时x的集合；
（3）求f（x）在$x∈[0，\frac{π}{2}]$时的值域．
13．已知函数f（2x）=x•log32，则f（39）的值为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{9}$ | C． | 6 | D． | 9 |
17．某单位要在800名员工中抽去80名员工调查职工身体健康状况，其中青年员工400名，中年员工300名，老年员工100名，下列说法错误的是（ ）
| A． | 老年人应作为重点调查对象，故抽取的老年人应超过40名 | |
| B． | 每个人被抽到的概率相同为$\frac{1}{10}$ | |
| C． | 应使用分层抽样抽取样本调查 | |
| D． | 抽出的样本能在一定程度上反映总体的健康状况 |